Basic statistics

Basics of
Statistics
By
Ganesh Raju

What is Statistics?
“Statistics is concerned with the inferential process, in particular with planning and
analysis of experiments or surveys, with the nature of observational errors and sources of
variability that obscure underlying patters, and with efficient summarizing of set of data”
= Kruskal
Why should we use statistics?
Statistical methods are required to ensure that data are interpreted correctly and the
apparent relationship are meaningful and not simply chance occurrence.
Statistics in Different Field
1. Business
2. Economics
3. Banking
4. Accounts and Auditing etc.,
Every day example…
1. Weather forecast
2. Emergency preparedness
3. Predicting diseases
4. Medical study
5. Political campaigns etc.,

Types of Data
Qualitative Quantitative
Discrete Continuous

• Qualitative Data
Qualitative data can be arranged into categories that are non numerical. These
categories can be physical traits, gender, colors or anything that does not have a number
associated to it. Qualitative data is sometimes referred to as categorical data
•Examples:
•Hair color (black, brown, blonde, white, grey, mahogany)
•Make of car (Dodge, Honda, Ford, Toyota)
•Gender (male, female)
•Place of birth (Riyadh, Jeddah, Yanbu)

• Quantitative Data
Quantitative data are measures of values or counts and are
expressed in numeric variables.
Examples:
For each orange tree, the number of oranges is measured
For a particular day, the number of cars entering a college
campus is measured
Time until a light bulb burns out
Etc.,

Four Basic Scale of Measurement

Nominal Scale:
This scale is the crudest among all measurement scales but is also the simplest scale.
In this scale the different scores on a measurement simply indicate different
categories.
The nominal scale is often referred to as a categorical scale. The assigned numbers
have no arithmetic properties and act only as labels. The only statistical operation that
can be performed on nominal scales is a frequency count. We cannot determine an
average except mode.
Examples:
Gender (1= male, 0=female)
ZIP code (7000=Philippines, …)
Plate numbers of vehicles (JK3429, MC001, …)
Course (Biology, Mathematics, History, …)
Race (Asian, American, …)
Eye color (Brown, Blue, …)

Ordinal Scale:
It involves the ranking of items along the continuum of the characteristic being scales.
In this scale, the items are classified according to whether they have more or less of
characteristic.
The main characteristic of the ordinal scale is that the categories have a logical or
ordered relationship. This type of scale permits the measurement of degrees of
difference, (i.e. 'more’ or ‘less’) but not the specific amount of differences (i.e. how
much ‘more’ or ‘less’).
Examples:
Ranks in a race (first, second, third, …)
Sizes of shirts (small, medium, large, …)
Order of birth (first child, second child , third child , …)
Socio-economic status (lower, middle, upper, …)
Difficulty level of a test (easy, average, difficult, …)
Degree of agreement (SD, D, A, SA)

Interval scale
Interval scale is a scale in which the numbers are used to rank attributes such that
numerically equal distance on the scale represent equal distance in the characteristic
being measured. An interval scale contains all the information of an ordinal scale, but
it also one allows to compare the difference/distance between attributes. Interval
scales may be either in numeric or semantic formats.
Examples:
Temperature (in oF or oC)
IQ Scores

Ratio scale
The highest scale, it allows the researcher to identify or classify objects, and compare
intervals or differences. It is also meaningful to compute ratios of scale values.
Is a possesses all the properties of the nomincal, ordinal and interval scale and in
addition an absolute zero point.
It is also meaningful to compute ratios of scale values. In the marketing , sales, costs,
market share and number of customers are available measure on ratio scale.
Examples:
I. Height (165cm, 154cm, 144cm, …)
II. Reaction time (20sec, 43sec, 37sec, …)
III. Number of siblings (2, 5, 8, …)
IV. Hours spent on studying for an exam (0, 2, 3, …)

Discrete and Continuous Data
 Numerical data could be either discrete or continuous.
 Continuous data can take any numerical value (within a range);
For example, weight, height, etc.,
 There can be an infinite number of possible values in continuous
data.
 Discrete data can take only certain values by a finite ;jumps;, i., it
‘jumps’ from one value to another but does not take any
intermediate value between them (For example, umber of
students in the class)

Example for Discrete and Continuous Data
A good example to distinguish discrete data from continuous data
is digital and analogue meter or clock were digital is discrete and
analog is continuous.

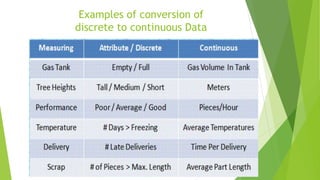
Examples of conversion of
discrete to continuous Data

Area of Statistics
Descriptive statistical limits generalization to
the particular group of individuals observed.
That is:
1. No conclusions are extended beyond
this group
2. Any similarity to those outside the
group cannot be assumed.
3. The data describe one group and that
group only.
Example: Assessment findings, findings a
much simpler action research.
Inferential analysis selects a small group out
of larger group an the findings are applied to
the larger group. It is used to estimate a
parameter, the corresponding value in the
population from the which the sample is
selected.
It is necessary to carefully select the sample
or the inferences may not apply to the
population.

Measures of Central Tendency and Dispersion

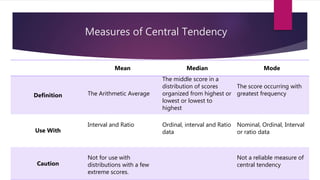
Measures of Central Tendency
Mean Median Mode
Definition The Arithmetic Average
The middle score in a
distribution of scores
organized from highest or
lowest or lowest to
highest
The score occurring with
greatest frequency
Use With
Interval and Ratio Ordinal, interval and Ratio
data
Nominal, Ordinal, Interval
or ratio data
Caution
Not for use with
distributions with a few
extreme scores.
Not a reliable measure of
central tendency

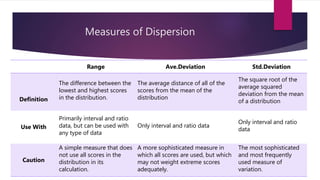
Measures of Dispersion
Range Ave.Deviation Std.Deviation
Definition
The difference between the
lowest and highest scores
in the distribution.
The average distance of all of the
scores from the mean of the
distribution
The square root of the
average squared
deviation from the mean
of a distribution
Use With
Primarily interval and ratio
data, but can be used with
any type of data
Only interval and ratio data
Only interval and ratio
data
Caution
A simple measure that does
not use all scores in the
distribution in its
calculation.
A more sophisticated measure in
which all scores are used, but which
may not weight extreme scores
adequately.
The most sophisticated
and most frequently
used measure of
variation.

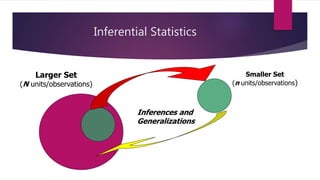
Inferential Statistics
Inferences and
Generalizations
Smaller Set
(n units/observations)
Larger Set
(N units/observations)

https://w55e7twkl7vq3lexl8-s-a2157.bj.tsgdht.cn/kotharivr/02-descriptive-statistics

Basic statistics

More Related Content

What's hot (20)

Similar to Basic statistics (20)

Recently uploaded (20)

Basic statistics