Business statistics solved numericals
Download as PPTX, PDF6 likes11,340 views
The document contains sample questions from previous years' business statistics exams. It includes two questions: 1) A question from 2006 that involves calculating the mean, standard deviation, and coefficient of variation for age data grouped into classes with frequency counts. 2) A question from 2007 that involves calculating the mean and median income from frequency data grouped into classes. The document shows the work and calculations to arrive at the answers for both questions.
Business statistics solved numericals
- 1. Business Statistics NMBA015 Previous Years’ Questions (Numerical) Unit I
- 2. Measures of Central Tendency
- 3. Measures of Central Tendency • Mean: 3 (2006, 2007, 2010) • Median: 1 (2007) • Missing Frequency: 1 (2009) • Combined Mean: 1 (2009) • Quartiles, Deciles, Percentiles: 1 (2012) • Total: 7
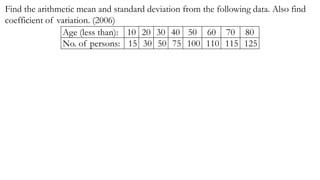
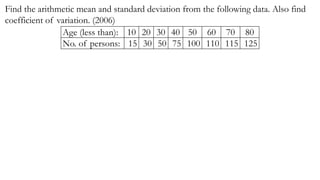
- 4. Find the arithmetic mean and standard deviation from the following data. Also find coefficient of variation. (2006) Age (less than): 10 20 30 40 50 60 70 80 No. of persons: 15 30 50 75 100 110 115 125
- 5. 𝐹𝑖𝑟𝑠𝑡 𝑤𝑒 𝑛𝑒𝑒𝑑 𝑡𝑜 𝑐𝑜𝑛𝑠𝑡𝑟𝑢𝑐𝑡 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠𝑒𝑠 𝑎𝑛𝑑 𝑐𝑜𝑚𝑝𝑢𝑡𝑒 𝑡ℎ𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠 𝑓𝑟𝑜𝑚 𝑡ℎ𝑒 𝑔𝑖𝑣𝑒𝑛 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠: 𝑁𝑜𝑡𝑒: 𝑆𝑖𝑛𝑐𝑒 𝑎𝑔𝑒 𝑐𝑎𝑛𝑛𝑜𝑡 𝑏𝑒 𝑙𝑒𝑠𝑠 𝑡ℎ𝑎𝑛 0, 𝑡ℎ𝑒𝑟𝑒𝑓𝑜𝑟𝑒 𝑡ℎ𝑒 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑙𝑜𝑤𝑒𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑐𝑎𝑛 𝑏𝑒 𝑡𝑎𝑘𝑒𝑛 𝑡𝑜 𝑏𝑒 𝑒𝑞𝑢𝑎𝑙 𝑡𝑜 0 𝐿𝑒𝑠𝑠 𝑡ℎ𝑎𝑛 𝑁𝑢𝑚𝑏𝑒𝑟 𝐶𝑙𝑎𝑠𝑠 𝑓 10 15 0 − 10 15 20 30 10 − 20 15 30 50 20 − 30 20 40 75 30 − 40 25 50 100 40 − 50 25 60 110 50 − 60 10 70 115 60 − 70 5 80 125 70 − 80 10 𝑁 = 125
- 6. 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑀𝑒𝑎𝑛: 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑋 𝑑𝑥 𝑑 𝑓𝑑 0 − 10 15 5 −40 −4 −60 10 − 20 15 15 −30 −3 −45 20 − 30 20 25 −20 −2 −40 30 − 40 25 35 −10 −1 −25 40 − 50 25 45 0 0 0 50 − 60 10 55 10 1 10 60 − 70 5 65 20 2 10 70 − 80 10 75 20 3 30 𝑁 = 125 Σ𝑓𝑑 = −120 𝑋 = 𝐴 + Σ𝑓𝑑 𝑁 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐴 = 𝑎𝑠𝑠𝑢𝑚𝑒𝑑 𝑚𝑒𝑎𝑛 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑑 = 𝑠𝑡𝑒𝑝 − 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 = 𝑑 𝑥 𝑖 = 𝑋 − 𝐴 𝑖 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑜. 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑖 = 𝑐𝑜𝑚𝑚𝑜𝑛 𝑓𝑎𝑐𝑡𝑜𝑟 𝐿𝑒𝑡 𝐴 = 45 𝐿𝑒𝑡 𝑖 = 10 𝑋 = 𝐴 + Σ𝑓𝑑 𝑁 × 𝑖 = 45 + −120 125 × 10 = 45 − 9.6 = 35.4
- 7. 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝐷𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝐶𝑉: 𝐴 = 45, 𝑖 = 10 𝜎 = (∑𝑓𝑑2) 𝑁 − ∑𝑓𝑑 𝑁 2 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑑 = 𝑠𝑡𝑒𝑝 − 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 = 𝑑 𝑥 𝑖 = 𝑋 − 𝐴 𝑖 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑜. 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑖 = 𝑐𝑜𝑚𝑚𝑜𝑛 𝑓𝑎𝑐𝑡𝑜𝑟 𝐶𝑉 = 𝜎 𝑋 × 100 𝑓 𝑋 𝑑 𝑓𝑑 𝑑2 𝑓𝑑2 15 5 −4 −60 16 240 15 15 −3 −45 9 135 20 25 −2 −40 4 80 25 35 −1 −25 1 25 25 45 0 0 0 0 10 55 1 10 1 10 5 65 2 10 4 20 10 75 3 30 9 90 𝑁 = 125 Σ𝑓𝑑 = −120 Σ𝑓𝑑2 = 600
- 8. 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝐷𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝐶𝑉: 𝜎 = 600 125 − −120 125 2 × 10 = 4.8 − 0.9216 × 10 = 3.8784 × 10 = 1.9694 × 10 = 19.694 𝐶𝑜𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡 𝑜𝑓 𝑉𝑎𝑟𝑖𝑎𝑡𝑖𝑜𝑛: 𝐶𝑉 = 𝜎 𝑋 × 100 = 19.694 35.4 × 100 = 55.6328 𝑨𝒏𝒔: 𝑴𝒆𝒂𝒏 = 𝟑𝟓. 𝟒, 𝑺𝒕𝒂𝒏𝒅𝒂𝒓𝒅 𝑫𝒆𝒗𝒊𝒂𝒕𝒊𝒐𝒏 = 𝟏𝟗. 𝟔𝟗𝟒, 𝑪𝑽 = 𝟓𝟓. 𝟔𝟑𝟐𝟖
- 9. Compute mean and median from the following data: (2007) Income more than (in Rs.): 1000 2000 3000 4000 5000 6000 7000 8000 No. of persons: 72 67 59 50 36 29 4 0
- 10. 𝐹𝑖𝑟𝑠𝑡 𝑤𝑒 𝑛𝑒𝑒𝑑 𝑡𝑜 𝑐𝑜𝑛𝑠𝑡𝑟𝑢𝑐𝑡 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠𝑒𝑠 𝑎𝑛𝑑 𝑐𝑜𝑚𝑝𝑢𝑡𝑒 𝑡ℎ𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠 𝑓𝑟𝑜𝑚 𝑡ℎ𝑒 𝑔𝑖𝑣𝑒𝑛 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠: 𝑀𝑜𝑟𝑒 𝑡ℎ𝑎𝑛 𝑁𝑢𝑚𝑏𝑒𝑟 𝐶𝑙𝑎𝑠𝑠 𝑓 1000 72 1000 − 2000 5 2000 67 2000 − 3000 8 3000 59 3000 − 4000 9 4000 50 4000 − 5000 14 5000 36 5000 − 6000 7 6000 29 6000 − 7000 25 7000 4 7000 − 8000 4 8000 0 𝑁 = 72
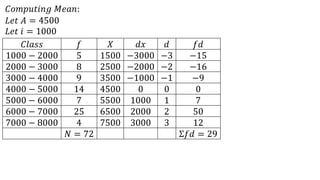
- 11. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝑀𝑒𝑎𝑛: 𝐿𝑒𝑡 𝐴 = 4500 𝐿𝑒𝑡 𝑖 = 1000 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑋 𝑑𝑥 𝑑 𝑓𝑑 1000 − 2000 5 1500 −3000 −3 −15 2000 − 3000 8 2500 −2000 −2 −16 3000 − 4000 9 3500 −1000 −1 −9 4000 − 5000 14 4500 0 0 0 5000 − 6000 7 5500 1000 1 7 6000 − 7000 25 6500 2000 2 50 7000 − 8000 4 7500 3000 3 12 𝑁 = 72 Σ𝑓𝑑 = 29
- 12. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝑀𝑒𝑎𝑛: 𝑋 = 𝐴 + Σ𝑓𝑑 𝑁 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐴 = 𝑎𝑠𝑠𝑢𝑚𝑒𝑑 𝑚𝑒𝑎𝑛 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑑 = 𝑠𝑡𝑒𝑝 − 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 = 𝑑 𝑥 𝑖 = 𝑋 − 𝐴 𝑖 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑖 = 𝑐𝑜𝑚𝑚𝑜𝑛 𝑓𝑎𝑐𝑡𝑜𝑟 𝐿𝑒𝑡 𝐴 = 4500 𝐿𝑒𝑡 𝑖 = 1000 𝑋 = 𝐴 + Σ𝑓𝑑 𝑁 × 𝑖 = 4500 + 29 72 × 1000 = 4500 + 402.7778 = 4902.7778
- 13. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝑀𝑒𝑑𝑖𝑎𝑛: 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑐𝑓 1000 − 2000 5 5 2000 − 3000 8 13 3000 − 4000 9 22 4000 − 5000 14 36 5000 − 6000 7 43 6000 − 7000 25 68 7000 − 8000 4 72 𝑁 = 72 𝑀 = 𝐿1 + 𝑁 2 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 − 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝐼𝑑𝑒𝑛𝑡𝑖𝑓𝑦𝑖𝑛𝑔 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠: 𝑁 2 = 72 2 = 36
- 14. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝑀𝑒𝑑𝑖𝑎𝑛: 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑐𝑓 1000 − 2000 5 5 2000 − 3000 8 13 3000 − 4000 9 22 4000 − 5000 14 36 5000 − 6000 7 43 6000 − 7000 25 68 7000 − 8000 4 72 𝑁 = 72 𝐼𝑑𝑒𝑛𝑡𝑖𝑓𝑦𝑖𝑛𝑔 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠: 𝑁 2 = 72 2 = 36 𝑇ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 𝑜𝑟 𝑒𝑞𝑢𝑎𝑙 𝑡𝑜 𝑁 2 , 𝑖. 𝑒. , 36 = 36 ∴ 𝑡ℎ𝑒 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑐𝑙𝑎𝑠𝑠, 𝑖. 𝑒. , 4000 − 5000 𝑖𝑠 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑀 = 𝐿1 + 𝑁 2 − 𝑐𝑓 𝑓 × 𝑖 𝐿1 = 4000, 𝑁 = 72, 𝑐𝑓 = 22, 𝑓 = 14, 𝑖 = 1000 ∴ 𝑀 = 4000 + 72 2 − 22 14 × 1000 = 4000 + 36 − 22 14 × 1000 = 4000 + 14 14 × 1000 = 4000 + 1000 = 5000 𝑨𝒏𝒔𝒘𝒆𝒓: 𝑴𝒆𝒂𝒏 = 𝟒𝟗𝟎𝟐. 𝟕𝟕𝟕𝟖 𝑴𝒆𝒅𝒊𝒂𝒏 = 𝟓𝟎𝟎𝟎
- 15. An incomplete frequency distribution is given as follows. Given that the median value is 46, determine the missing frequencies using the median formula. (2009) Variable 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Total Frequency 12 30 ? 65 ? 25 18 229
- 16. 𝐿𝑒𝑡 𝑢𝑠 𝑎𝑠𝑠𝑢𝑚𝑒 𝑡ℎ𝑒 𝑚𝑖𝑠𝑠𝑖𝑛𝑔 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠 𝑎𝑠 𝑥 𝑎𝑛𝑑 𝑦, 𝑟𝑒𝑠𝑝𝑒𝑐𝑡𝑖𝑣𝑒𝑙𝑦 𝑇ℎ𝑒 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝑖𝑡𝑠 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠 𝑐𝑎𝑛 𝑏𝑒 𝑤𝑟𝑖𝑡𝑡𝑒𝑛 𝑎𝑠 𝑓𝑜𝑙𝑙𝑜𝑤𝑠: 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑐𝑓 10 − 20 12 12 20 − 30 30 42 30 − 40 𝑥 42 + 𝑥 40 − 50 65 107 + 𝑥 50 − 60 𝑦 107 + 𝑥 + 𝑦 60 − 70 25 132 + 𝑥 + 𝑦 70 − 80 18 150 + 𝑥 + 𝑦 𝑁 = 229 𝑊𝑒 𝑘𝑛𝑜𝑤 𝑡ℎ𝑎𝑡 𝑚𝑒𝑑𝑖𝑎𝑛, 𝑀 = 𝐿1 + 𝑁 2 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 − 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠
- 17. ∵ 𝑖𝑡 𝑖𝑠 𝑔𝑖𝑣𝑒𝑛 𝑡ℎ𝑎𝑡 𝑀 = 46 ∴ 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 = 40 − 50 ∴ 𝐿1 = 40, 𝑁 𝑔𝑖𝑣𝑒𝑛 = 229, 𝑐𝑓 = 42 + 𝑥, 𝑓 = 65, 𝑖 = 50 − 40 = 10 𝑃𝑢𝑡𝑡𝑖𝑛𝑔 𝑡ℎ𝑒 𝑣𝑎𝑙𝑢𝑒𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑓𝑜𝑟𝑚𝑢𝑙𝑎: 46 = 40 + 229 2 − 42 + 𝑥 65 × 10 𝑜𝑟 229 2 − 42 + 𝑥 65 × 10 = 46 − 40 𝑜𝑟 229 2 − 42 + 𝑥 65 × 10 = 6 𝑜𝑟 229 2 − 42 + 𝑥 = 6 × 65 10 𝑜𝑟 229 2 − 42 − 𝑥 = 39
- 18. 𝑜𝑟 𝑥 = 229 2 − 42 − 39 = 33.5 ≃ 34 𝑁𝑜𝑤, 𝑡ℎ𝑒 𝑙𝑎𝑠𝑡 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 = 𝑁 ∴ 150 + 𝑥 + 𝑦 = 229 𝑜𝑟 150 + 34 + 𝑦 = 229 𝑜𝑟 𝑦 = 229 − 150 − 34 = 45 𝑨𝒏𝒔: 𝑻𝒉𝒆 𝒎𝒊𝒔𝒔𝒊𝒏𝒈 𝒇𝒓𝒆𝒒𝒖𝒆𝒏𝒄𝒊𝒆𝒔 𝒂𝒓𝒆 𝟑𝟒 𝒂𝒏𝒅 𝟒𝟓, 𝒓𝒆𝒔𝒑𝒆𝒄𝒕𝒊𝒗𝒆𝒍𝒚
- 19. The mean annual salary of employees of a company is Rs.30000. The mean annual salaries of male and female employees are Rs.35000 and Rs.23000, respectively. Find out the percentage of male and female employees working in the company. (2009)
- 20. 𝐿𝑒𝑡 𝑡ℎ𝑒 𝑝𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝑜𝑓 𝑚𝑎𝑙𝑒 𝑒𝑚𝑝𝑙𝑜𝑦𝑒𝑒𝑠 𝑏𝑒 𝑥 𝑇ℎ𝑒𝑛 𝑡ℎ𝑒 𝑝𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝑜𝑓 𝑓𝑒𝑚𝑎𝑙𝑒 𝑒𝑚𝑝𝑙𝑜𝑦𝑒𝑒𝑠 𝑤𝑖𝑙𝑙 𝑏𝑒 100 − 𝑥 𝐿𝑒𝑡 𝑚𝑒𝑎𝑛 𝑎𝑛𝑛𝑢𝑎𝑙 𝑠𝑎𝑙𝑎𝑟𝑦 𝑜𝑓 𝑎𝑙𝑙 𝑒𝑚𝑝𝑙𝑜𝑦𝑒𝑒𝑠 𝑏𝑒 𝑑𝑒𝑛𝑜𝑡𝑒𝑑 𝑏𝑦 𝑋 𝐿𝑒𝑡 𝑚𝑒𝑎𝑛 𝑎𝑛𝑛𝑢𝑎𝑙 𝑠𝑎𝑙𝑎𝑟𝑦 𝑜𝑓 𝑎𝑙𝑙 𝑚𝑎𝑙𝑒 𝑒𝑚𝑝𝑙𝑜𝑦𝑒𝑒𝑠 𝑏𝑒 𝑑𝑒𝑛𝑜𝑡𝑒𝑑 𝑏𝑦 𝑋 𝑀 𝐿𝑒𝑡 𝑚𝑒𝑎𝑛 𝑎𝑛𝑛𝑢𝑎𝑙 𝑠𝑎𝑙𝑎𝑟𝑦 𝑜𝑓 𝑎𝑙𝑙 𝑓𝑒𝑚𝑎𝑙𝑒 𝑒𝑚𝑝𝑙𝑜𝑦𝑒𝑒𝑠 𝑏𝑒 𝑑𝑒𝑛𝑜𝑡𝑒𝑑 𝑏𝑦 𝑋 𝐹 𝑇ℎ𝑒𝑛, 𝑋 = 𝑋 𝑀 × % 𝑜𝑓 𝑚𝑎𝑙𝑒 𝑒𝑚𝑝𝑙𝑜𝑦𝑒𝑒𝑠 + 𝑋 𝐹 × % 𝑜𝑓 𝑚𝑎𝑙𝑒 𝑒𝑚𝑝𝑙𝑜𝑦𝑒𝑒𝑠 100 𝑜𝑟 30000 = 35000 × 𝑥 + 23000 100 − 𝑥 100 𝑜𝑟 35000𝑥 + 23000 100 − 𝑥 = 30000 × 100 𝑜𝑟 35000𝑥 + 2300000 − 23000𝑥 = 3000000 𝑜𝑟 12000𝑥 = 3000000 − 2300000 𝑜𝑟 12000𝑥 = 700000 𝑜𝑟 𝑥 = 700000 12000 = 58.33% 100 − 𝑥 = 100 − 58.33 = 41.67%
- 21. 𝑨𝒏𝒔: 𝑷𝒆𝒓𝒄𝒆𝒏𝒕𝒂𝒈𝒆 𝒐𝒇 𝒎𝒂𝒍𝒆 𝒆𝒎𝒑𝒍𝒐𝒚𝒆𝒆𝒔 𝒘𝒐𝒓𝒌𝒊𝒏𝒈 𝒊𝒏 𝒕𝒉𝒆 𝒄𝒐𝒎𝒑𝒂𝒏𝒚 = 𝟓𝟖. 𝟑𝟑% 𝑷𝒆𝒓𝒄𝒆𝒏𝒕𝒂𝒈𝒆 𝒐𝒇 𝒇𝒆𝒎𝒂𝒍𝒆 𝒆𝒎𝒑𝒍𝒐𝒚𝒆𝒆𝒔 𝒘𝒐𝒓𝒌𝒊𝒏𝒈 𝒊𝒏 𝒕𝒉𝒆 𝒄𝒐𝒎𝒑𝒂𝒏𝒚 = 𝟒𝟏. 𝟔𝟕%
- 22. 8 coins are tossed at a time, 256 times. The actual results of getting the numbers of heads are as follows. Find out expected frequencies. Also calculate mean and standard deviation. (2010) No. of Heads: 0 1 2 3 4 5 6 7 8 Total Frequency: 2 6 30 52 67 56 32 10 1 256
- 23. 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑒𝑥𝑝𝑒𝑐𝑡𝑒𝑑 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠: 𝐸𝑥𝑝𝑒𝑐𝑡𝑒𝑑 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 = 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑡𝑖𝑚𝑒𝑠 𝑒𝑥𝑝𝑒𝑟𝑖𝑚𝑒𝑛𝑡 𝑖𝑠 𝑟𝑒𝑝𝑒𝑎𝑡𝑒𝑑 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑝𝑜𝑠𝑠𝑖𝑏𝑙𝑒 𝑜𝑢𝑡𝑐𝑜𝑚𝑒𝑠 = 256 9 = 28.44 𝐶𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑖𝑛𝑔 𝑚𝑒𝑎𝑛: 𝑋 𝑓 𝑑 𝑥 𝑓𝑑 𝑥 0 2 −4 -8 1 6 -3 -18 2 30 -2 -60 3 52 -1 -52 4 67 0 0 5 56 1 56 6 32 2 64 7 10 3 30 8 1 4 4 𝑁 = 256 Σ𝑓𝑑 𝑥 = 16 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑚𝑒𝑎𝑛 𝑢𝑠𝑖𝑛𝑔 𝑡ℎ𝑒 𝑠ℎ𝑜𝑟𝑡 − 𝑐𝑢𝑡 𝑚𝑒𝑡ℎ𝑜𝑑: 𝑋 = 𝐴 + Σ𝑓𝑑 𝑥 𝑁 𝐿𝑒𝑡 𝐴 = 4 𝑋 = 4 + 16 256 = 4 + 0.0625 = 4.0625
- 24. 𝑋 𝑓 𝑑 𝑥 𝑓𝑑 𝑥 𝑑 𝑥 2 𝑓𝑑 𝑥 2 0 2 −4 -8 16 32 1 6 -3 -18 9 54 2 30 -2 -60 4 120 3 52 -1 -52 1 52 4 67 0 0 0 0 5 56 1 56 1 56 6 32 2 64 4 128 7 10 3 30 9 90 8 1 4 4 16 16 𝑁 = 256 Σ𝑓𝑑 𝑥 = 16 ∑𝑓𝑑 𝑥 2 = 548 𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑠ℎ𝑜𝑟𝑡 − 𝑐𝑢𝑡 𝑚𝑒𝑡ℎ𝑜𝑑 : 𝜎 = (∑𝑓𝑑 𝑥 2 ) 𝑁 − ∑𝑓𝑑 𝑥 𝑁 2 = 548 256 − 16 256 2 = 2.1406 − 0.0039 = 2.1367 = 1.4617
- 25. Find the Q3, D7 and P69 of the following: (2012) Variable 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Frequency 7 12 18 25 16 14 8
- 26. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝑄3, 𝐷7 𝑎𝑛𝑑 𝑃69: 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑐𝑓 0 − 10 7 7 10 − 20 12 19 20 − 30 18 37 30 − 40 25 62 40 − 50 16 78 50 − 60 14 92 60 − 70 8 100 𝑁 = 100 𝑄3 = 𝐿1 + 3𝑁 4 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑄3 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑄3 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑄3 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝑄3 𝑐𝑙𝑎𝑠𝑠 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑄3 𝑐𝑙𝑎𝑠𝑠: 3𝑁 4 = 3 × 100 4 = 300 4 = 75 ∵ 40 − 50 𝑖𝑠 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑤𝑖𝑡ℎ 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 75 𝑖. 𝑒. , 78 ∴ 40 − 50 𝑖𝑠 𝑡ℎ𝑒 𝑄3 𝑐𝑙𝑎𝑠𝑠 ∴ 𝐿1 = 40, 𝑁 = 100, 𝑐𝑓 = 62, 𝑓 = 16, 𝑖 = 50 − 40
- 27. 𝑄3 = 𝐿1 + 3𝑁 4 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑄3 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑄3 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑄3 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝑄3 𝑐𝑙𝑎𝑠𝑠 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑄3 𝑐𝑙𝑎𝑠𝑠: 3𝑁 4 = 3 × 100 4 = 300 4 = 75 ∵ 40 − 50 𝑖𝑠 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑤𝑖𝑡ℎ 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 75 𝑖. 𝑒. , 78 ∴ 40 − 50 𝑖𝑠 𝑡ℎ𝑒 𝑄3 𝑐𝑙𝑎𝑠𝑠 ∴ 𝐿1 = 40, 𝑁 = 100, 𝑐𝑓 = 62, 𝑓 = 16, 𝑖 = 50 − 40 = 10 ∴ 𝑄3 = 40 + 3 × 100 4 − 62 16 × 10 = 40 + 75 − 62 16 × 10 = 40 + 13 16 × 10 = 40 + 8.125 = 48.125
- 28. 𝐷7 = 𝐿1 + 7𝑁 10 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝐷7 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝐷7 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝐷7 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝐷7 𝑐𝑙𝑎𝑠𝑠 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝐷7 𝑐𝑙𝑎𝑠𝑠: 7𝑁 10 = 7 × 100 10 = 700 10 = 70 ∵ 40 − 50 𝑖𝑠 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑤𝑖𝑡ℎ 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 70 ∴ 40 − 50 𝑖𝑠 𝑡ℎ𝑒 𝐷7 𝑐𝑙𝑎𝑠𝑠 ∴ 𝐿1 = 40, 𝑁 = 100, 𝑐𝑓 = 62, 𝑓 = 16, 𝑖 = 10 ∴ 𝐷7 = 40 + 7 × 100 10 − 62 16 × 10 = 40 + 70 − 62 16 × 10 = 40 + 8 16 × 10 = 40 + 5 = 45
- 29. 𝑃69 = 𝐿1 + 69𝑁 100 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑃69 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑃69 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑃69 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝑃69 𝑐𝑙𝑎𝑠𝑠 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑃69 𝑐𝑙𝑎𝑠𝑠: 69𝑁 100 = 69 × 100 100 = 69 ∵ 40 − 50 𝑖𝑠 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑤𝑖𝑡ℎ 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 69 ∴ 40 − 50 𝑖𝑠 𝑡ℎ𝑒 𝑃69 𝑐𝑙𝑎𝑠𝑠 ∴ 𝐿1 = 40, 𝑁 = 100, 𝑐𝑓 = 62, 𝑓 = 16, 𝑖 = 10 ∴ 𝑃69 = 40 + 69 × 100 100 − 62 16 × 10 = 40 + 69 − 62 16 × 10 = 40 + 7 16 × 10 = 40 + 4.375 = 43.375
- 31. Measures of Dispersion • Standard Deviation: 3 (2004, 2006, 2010) • Coefficient of Variation: 4 (2005, 2006, 2008, 2012) • Total: 7
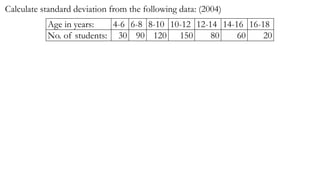
- 32. Calculate standard deviation from the following data: (2004) Age in years: 4-6 6-8 8-10 10-12 12-14 14-16 16-18 No. of students: 30 90 120 150 80 60 20
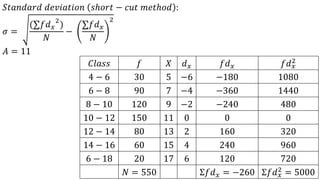
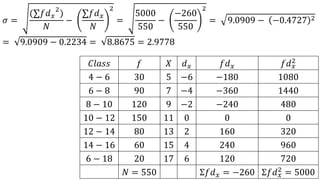
- 33. 𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑠ℎ𝑜𝑟𝑡 − 𝑐𝑢𝑡 𝑚𝑒𝑡ℎ𝑜𝑑 : 𝜎 = (∑𝑓𝑑 𝑥 2 ) 𝑁 − ∑𝑓𝑑 𝑥 𝑁 2 𝐴 = 11 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑋 𝑑 𝑥 𝑓𝑑 𝑥 𝑓𝑑 𝑥 2 4 − 6 30 5 −6 −180 1080 6 − 8 90 7 −4 −360 1440 8 − 10 120 9 −2 −240 480 10 − 12 150 11 0 0 0 12 − 14 80 13 2 160 320 14 − 16 60 15 4 240 960 6 − 18 20 17 6 120 720 𝑁 = 550 Σ𝑓𝑑 𝑥 = −260 Σ𝑓𝑑 𝑥 2 = 5000
- 34. 𝜎 = (∑𝑓𝑑 𝑥 2 ) 𝑁 − ∑𝑓𝑑 𝑥 𝑁 2 = 5000 550 − −260 550 2 = 9.0909 − −0.4727 2 = 9.0909 − 0.2234 = 8.8675 = 2.9778 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑋 𝑑 𝑥 𝑓𝑑 𝑥 𝑓𝑑 𝑥 2 4 − 6 30 5 −6 −180 1080 6 − 8 90 7 −4 −360 1440 8 − 10 120 9 −2 −240 480 10 − 12 150 11 0 0 0 12 − 14 80 13 2 160 320 14 − 16 60 15 4 240 960 6 − 18 20 17 6 120 720 𝑁 = 550 Σ𝑓𝑑 𝑥 = −260 Σ𝑓𝑑 𝑥 2 = 5000
- 35. Find the coefficient of variation, if the sum of squares of the deviations of 10 observations taken from mean 50 is 250. (2005) 𝐺𝑖𝑣𝑒𝑛 𝑡ℎ𝑎𝑡: 𝑁 = 10, 𝑋 = 50, Σ𝑑 𝑥 2 = 250 𝐶𝑉 = 𝜎 𝑋 × 100 𝜎 = Σ𝑑 𝑥 2 𝑁 ∴ 𝐶𝑉 = Σ𝑑 𝑥 2 𝑁 𝑋 × 100 = 250 10 50 × 100 = 25 50 × 100 = 5 50 × 100 = 10
- 36. Find the arithmetic mean and standard deviation from the following data. Also find coefficient of variation. (2006) Age (less than): 10 20 30 40 50 60 70 80 No. of persons: 15 30 50 75 100 110 115 125
- 37. 𝐹𝑖𝑟𝑠𝑡 𝑤𝑒 𝑛𝑒𝑒𝑑 𝑡𝑜 𝑐𝑜𝑛𝑠𝑡𝑟𝑢𝑐𝑡 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠𝑒𝑠 𝑎𝑛𝑑 𝑐𝑜𝑚𝑝𝑢𝑡𝑒 𝑡ℎ𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠 𝑓𝑟𝑜𝑚 𝑡ℎ𝑒 𝑔𝑖𝑣𝑒𝑛 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠: 𝑁𝑜𝑡𝑒: 𝑆𝑖𝑛𝑐𝑒 𝑎𝑔𝑒 𝑐𝑎𝑛𝑛𝑜𝑡 𝑏𝑒 𝑙𝑒𝑠𝑠 𝑡ℎ𝑎𝑛 0, 𝑡ℎ𝑒𝑟𝑒𝑓𝑜𝑟𝑒 𝑡ℎ𝑒 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑙𝑜𝑤𝑒𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑐𝑎𝑛 𝑏𝑒 𝑡𝑎𝑘𝑒𝑛 𝑡𝑜 𝑏𝑒 𝑒𝑞𝑢𝑎𝑙 𝑡𝑜 0 𝐿𝑒𝑠𝑠 𝑡ℎ𝑎𝑛 𝑁𝑢𝑚𝑏𝑒𝑟 𝐶𝑙𝑎𝑠𝑠 𝑓 10 15 0 − 10 15 20 30 10 − 20 15 30 50 20 − 30 20 40 75 30 − 40 25 50 100 40 − 50 25 60 110 50 − 60 10 70 115 60 − 70 5 80 125 70 − 80 10 𝑁 = 125
- 38. 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑀𝑒𝑎𝑛: 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑋 𝑑𝑥 𝑑 𝑓𝑑 0 − 10 15 5 −40 −4 −60 10 − 20 15 15 −30 −3 −45 20 − 30 20 25 −20 −2 −40 30 − 40 25 35 −10 −1 −25 40 − 50 25 45 0 0 0 50 − 60 10 55 10 1 10 60 − 70 5 65 20 2 10 70 − 80 10 75 20 3 30 𝑁 = 125 Σ𝑓𝑑 = −120 𝑋 = 𝐴 + Σ𝑓𝑑 𝑁 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐴 = 𝑎𝑠𝑠𝑢𝑚𝑒𝑑 𝑚𝑒𝑎𝑛 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑑 = 𝑠𝑡𝑒𝑝 − 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 = 𝑑 𝑥 𝑖 = 𝑋 − 𝐴 𝑖 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑜. 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑖 = 𝑐𝑜𝑚𝑚𝑜𝑛 𝑓𝑎𝑐𝑡𝑜𝑟 𝐿𝑒𝑡 𝐴 = 45 𝐿𝑒𝑡 𝑖 = 10 𝑋 = 𝐴 + Σ𝑓𝑑 𝑁 × 𝑖 = 45 + −120 125 × 10 = 45 − 9.6 = 35.4
- 39. 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝐷𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝐶𝑉: 𝐴 = 45, 𝑖 = 10 𝜎 = (∑𝑓𝑑2) 𝑁 − ∑𝑓𝑑 𝑁 2 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑑 = 𝑠𝑡𝑒𝑝 − 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 = 𝑑 𝑥 𝑖 = 𝑋 − 𝐴 𝑖 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑜. 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑖 = 𝑐𝑜𝑚𝑚𝑜𝑛 𝑓𝑎𝑐𝑡𝑜𝑟 𝐶𝑉 = 𝜎 𝑋 × 100 𝑓 𝑋 𝑑 𝑓𝑑 𝑑2 𝑓𝑑2 15 5 −4 −60 16 240 15 15 −3 −45 9 135 20 25 −2 −40 4 80 25 35 −1 −25 1 25 25 45 0 0 0 0 10 55 1 10 1 10 5 65 2 10 4 20 10 75 3 30 9 90 𝑁 = 125 Σ𝑓𝑑 = −120 Σ𝑓𝑑2 = 600
- 40. 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝐷𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝐶𝑉: 𝜎 = 600 125 − −120 125 2 × 10 = 4.8 − 0.9216 × 10 = 3.8784 × 10 = 1.9694 × 10 = 19.694 𝐶𝑜𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡 𝑜𝑓 𝑉𝑎𝑟𝑖𝑎𝑡𝑖𝑜𝑛: 𝐶𝑉 = 𝜎 𝑋 × 100 = 19.694 35.4 × 100 = 55.6328 𝑨𝒏𝒔: 𝑴𝒆𝒂𝒏 = 𝟑𝟓. 𝟒, 𝑺𝒕𝒂𝒏𝒅𝒂𝒓𝒅 𝑫𝒆𝒗𝒊𝒂𝒕𝒊𝒐𝒏 = 𝟏𝟗. 𝟔𝟗𝟒, 𝑪𝑽 = 𝟓𝟓. 𝟔𝟑𝟐𝟖
- 41. Share prices of two companies A Ltd. and B Ltd. were recorded as follows. Which company’s share prices are more variable? (2008, 2012) A Ltd. 12 13 15 14 14 14 13 17 B Ltd. 113 114 113 115 117 114 112 114
- 42. 𝐻𝑒𝑟𝑒, 𝑤𝑒 ℎ𝑎𝑣𝑒 𝑡𝑜 𝑓𝑖𝑛𝑑 𝑤ℎ𝑖𝑐ℎ 𝑐𝑜𝑚𝑝𝑎𝑛𝑦′ 𝑠 𝑠ℎ𝑎𝑟𝑒 𝑝𝑟𝑖𝑐𝑒𝑠 𝑎𝑟𝑒 𝑚𝑜𝑟𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒. 𝑇ℎ𝑒 𝑠𝑡𝑎𝑡𝑖𝑠𝑡𝑖𝑐𝑎𝑙 𝑚𝑒𝑎𝑠𝑢𝑟𝑒 𝑓𝑜𝑟 𝑣𝑎𝑟𝑖𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑖𝑠 𝑡ℎ𝑒 𝑚𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑑𝑖𝑠𝑝𝑒𝑟𝑠𝑖𝑜𝑛. 𝑇ℎ𝑒 𝑏𝑒𝑠𝑡 𝑚𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑑𝑖𝑠𝑝𝑒𝑟𝑠𝑖𝑜𝑛 𝑖𝑠 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛. 𝐻𝑜𝑤𝑒𝑣𝑒𝑟, 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑖𝑠 𝑎𝑛 𝑎𝑏𝑠𝑜𝑙𝑢𝑡𝑒 𝑚𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑑𝑖𝑠𝑝𝑒𝑟𝑠𝑖𝑜𝑛 𝑎𝑛𝑑 ℎ𝑒𝑛𝑐𝑒 𝑖𝑡 𝑐𝑎𝑛𝑛𝑜𝑡 𝑏𝑒 𝑢𝑠𝑒𝑑 𝑓𝑜𝑟 𝑐𝑜𝑚𝑝𝑎𝑟𝑖𝑠𝑜𝑛. ∴ 𝑖𝑛 𝑡ℎ𝑖𝑠 𝑐𝑎𝑠𝑒, 𝑓𝑜𝑟 𝑐𝑜𝑚𝑝𝑎𝑟𝑖𝑛𝑔 𝑡ℎ𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑠ℎ𝑎𝑟𝑒 𝑝𝑟𝑖𝑐𝑒𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑡𝑤𝑜 𝑐𝑜𝑚𝑝𝑎𝑝𝑖𝑒𝑠 𝑤𝑒 𝑠ℎ𝑎𝑙𝑙 𝑐𝑜𝑚𝑝𝑢𝑡𝑒 𝑡ℎ𝑒 𝑐𝑜𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡 𝑜𝑓 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑜𝑛 𝐶𝑉 , 𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 𝑡ℎ𝑒 𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑒 𝑚𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑑𝑖𝑠𝑝𝑒𝑟𝑠𝑖𝑜𝑛 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑡𝑜 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛. 𝑇ℎ𝑒 𝑐𝑜𝑚𝑝𝑎𝑛𝑦 𝑤𝑖𝑡ℎ 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝐶𝑉 𝑤𝑖𝑙𝑙 𝑏𝑒 ℎ𝑎𝑣𝑖𝑛𝑔 𝑚𝑜𝑟𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑠ℎ𝑎𝑟𝑒 𝑝𝑟𝑖𝑐𝑒𝑠.
- 43. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝐶𝑉 𝑓𝑜𝑟 𝐴 𝐿𝑡𝑑. : 𝑋 𝑑 𝑥 𝑑 𝑥 2 12 −2 4 13 −1 1 15 1 1 14 0 0 14 0 0 14 0 0 13 −1 1 17 3 9 112 16 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝑋: 𝑋𝐴 = Σ𝑋 𝑁 Σ𝑋 = 112, 𝑁 = 8 ∴ 𝑋𝐴 = 112 8 = 14 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝜎: 𝜎𝐴 = Σ𝑑 𝑥 2 𝑁 Σ𝑑 𝑥 2 = 16, 𝑁 = 8 ∴ 𝜎𝐴 = 16 8 = 2 = 1.414
- 44. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝐶𝑉 𝑓𝑜𝑟 𝐴 𝐿𝑡𝑑. : 𝐶𝑉 = 𝜎 𝑋 × 100 = 1.414 14 × 100 = 10.1
- 45. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝐶𝑉 𝑓𝑜𝑟 𝐵 𝐿𝑡𝑑. : 𝑋 𝑑 𝑥 𝑑 𝑥 2 113 −1 1 114 0 0 113 −1 1 115 1 1 117 3 9 114 0 0 112 −2 4 114 0 0 912 16 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝑋: 𝑋 𝐵 = Σ𝑋 𝑁 Σ𝑋 = 912, 𝑁 = 8 ∴ 𝑋 𝐵 = 912 8 = 114 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝜎: 𝜎 𝐵 = Σ𝑑 𝑥 2 𝑁 Σ𝑑 𝑥 2 = 16, 𝑁 = 8 ∴ 𝜎 𝐵 = 16 8 = 2 = 1.414
- 46. 𝐶𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔 𝐶𝑉 𝑓𝑜𝑟 𝐵 𝐿𝑡𝑑. : 𝐶𝑉 = 𝜎 𝑋 × 100 = 1.414 114 × 100 = 1.2404
- 47. 𝐶𝑉 𝑜𝑓 𝐴 𝐿𝑡𝑑. = 10.1 𝐶𝑉 𝑜𝑓 𝐵 𝐿𝑡𝑑. = 1.2404 ∵ 𝐶𝑉𝑜𝑓 𝐴 𝐿𝑡𝑑. 𝑖𝑠 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 𝑡ℎ𝑎𝑡 𝑜𝑓 𝐵 𝐿𝑡𝑑. ∴ 𝑤𝑒 𝑐𝑎𝑛 𝑐𝑜𝑛𝑐𝑙𝑢𝑑𝑒 𝑡ℎ𝑎𝑡 𝑡ℎ𝑒 𝑠ℎ𝑎𝑟𝑒 𝑝𝑟𝑖𝑐𝑒𝑠 𝑜𝑓 𝐵 𝐿𝑡𝑑. 𝑎𝑟𝑒 𝑚𝑜𝑟𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑡ℎ𝑎𝑛 𝑡ℎ𝑒 𝑠ℎ𝑎𝑟𝑒 𝑝𝑟𝑖𝑐𝑒𝑠 𝑜𝑓 𝐴 𝐿𝑡𝑑.
- 48. 8 coins are tossed at a time, 256 times. The actual results of getting the numbers of heads are as follows. Find out expected frequencies. Also calculate mean and standard deviation. (2010) No. of Heads: 0 1 2 3 4 5 6 7 8 Total Frequency: 2 6 30 52 67 56 32 10 1 256
- 49. 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑒𝑥𝑝𝑒𝑐𝑡𝑒𝑑 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑖𝑒𝑠: 𝐸𝑥𝑝𝑒𝑐𝑡𝑒𝑑 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 = 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑡𝑖𝑚𝑒𝑠 𝑒𝑥𝑝𝑒𝑟𝑖𝑚𝑒𝑛𝑡 𝑖𝑠 𝑟𝑒𝑝𝑒𝑎𝑡𝑒𝑑 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑝𝑜𝑠𝑠𝑖𝑏𝑙𝑒 𝑜𝑢𝑡𝑐𝑜𝑚𝑒𝑠 = 256 9 = 28.44 𝐶𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑖𝑛𝑔 𝑚𝑒𝑎𝑛: 𝑋 𝑓 𝑑 𝑥 𝑓𝑑 𝑥 0 2 −4 -8 1 6 -3 -18 2 30 -2 -60 3 52 -1 -52 4 67 0 0 5 56 1 56 6 32 2 64 7 10 3 30 8 1 4 4 𝑁 = 256 Σ𝑓𝑑 𝑥 = 16 𝐹𝑖𝑛𝑑𝑖𝑛𝑔 𝑚𝑒𝑎𝑛 𝑢𝑠𝑖𝑛𝑔 𝑡ℎ𝑒 𝑠ℎ𝑜𝑟𝑡 − 𝑐𝑢𝑡 𝑚𝑒𝑡ℎ𝑜𝑑: 𝑋 = 𝐴 + Σ𝑓𝑑 𝑥 𝑁 𝐿𝑒𝑡 𝐴 = 4 𝑋 = 4 + 16 256 = 4 + 0.0625 = 4.0625
- 50. 𝑋 𝑓 𝑑 𝑥 𝑓𝑑 𝑥 𝑑 𝑥 2 𝑓𝑑 𝑥 2 0 2 −4 -8 16 32 1 6 -3 -18 9 54 2 30 -2 -60 4 120 3 52 -1 -52 1 52 4 67 0 0 0 0 5 56 1 56 1 56 6 32 2 64 4 128 7 10 3 30 9 90 8 1 4 4 16 16 𝑁 = 256 Σ𝑓𝑑 𝑥 = 16 ∑𝑓𝑑 𝑥 2 = 548 𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑠ℎ𝑜𝑟𝑡 − 𝑐𝑢𝑡 𝑚𝑒𝑡ℎ𝑜𝑑 : 𝜎 = (∑𝑓𝑑 𝑥 2 ) 𝑁 − ∑𝑓𝑑 𝑥 𝑁 2 = 548 256 − 16 256 2 = 2.1406 − 0.0039 = 2.1367 = 1.4617
- 51. Measures of Skewness and Kurtosis
- 52. Measures of Skewness and Kurtosis • Skewness: 2 (2008, 2010) • Kurtosis: 1 (2010) • Total: 3
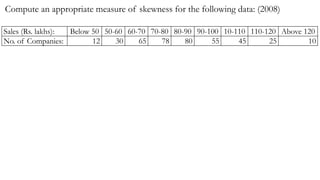
- 53. Compute an appropriate measure of skewness for the following data: (2008) Sales (Rs. lakhs): Below 50 50-60 60-70 70-80 80-90 90-100 10-110 110-120 Above 120 No. of Companies: 12 30 65 78 80 55 45 25 10
- 54. ∵ 𝑡ℎ𝑒 𝑑𝑎𝑡𝑎 𝑐𝑜𝑛𝑡𝑎𝑖𝑛𝑠 𝑜𝑝𝑒𝑛 − 𝑒𝑛𝑑𝑒𝑑 𝑐𝑙𝑎𝑠𝑠𝑒𝑠 ∴ 𝑚𝑒𝑎𝑛 𝑐𝑎𝑛𝑛𝑜𝑡 𝑏𝑒 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑 ∴ 𝑤𝑒 𝑐𝑎𝑛𝑛𝑜𝑡 𝑢𝑠𝑒 𝑎 𝑚𝑒𝑎𝑛 − 𝑏𝑎𝑠𝑒𝑑 𝑚𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑠𝑘𝑒𝑤𝑛𝑒𝑠𝑠 ∴ 𝑡ℎ𝑒 𝑚𝑜𝑠𝑡 𝑎𝑝𝑝𝑟𝑜𝑝𝑟𝑖𝑎𝑡𝑒 𝑚𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑠𝑘𝑒𝑤𝑛𝑒𝑠𝑠 𝑖𝑛 𝑡ℎ𝑖𝑠 𝑐𝑎𝑠𝑒 𝑤𝑜𝑢𝑙𝑑 𝑏𝑒 𝑡ℎ𝑒 𝐵𝑜𝑤𝑙𝑒𝑦′ 𝑠 𝑐𝑜𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡 𝑜𝑓 𝑠𝑘𝑒𝑤𝑛𝑒𝑠𝑠, 𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 𝑔𝑖𝑣𝑒𝑛 𝑏𝑦: 𝒋B = 𝑸3 + 𝑸1 − 𝟐𝑴 𝑸3 − 𝑸1 ∴ 𝑤𝑒 𝑛𝑒𝑒𝑑 𝑡𝑜 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒 𝑚𝑒𝑑𝑖𝑎𝑛, 𝑓𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑎𝑛𝑑 𝑡ℎ𝑖𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑀𝑒𝑑𝑖𝑎𝑛, 𝑀 = 𝐿1 + 𝑁 2 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 − 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠
- 55. 𝐹𝑖𝑟𝑠𝑡 𝑄𝑢𝑎𝑟𝑡𝑖𝑙𝑒, 𝑄1 = 𝐿1 + 𝑁 2 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑓𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑓𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 − 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝑓𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 𝑇ℎ𝑖𝑟𝑑 𝑄𝑢𝑎𝑟𝑡𝑖𝑙𝑒, 𝑄3 = 𝐿1 + 𝑁 2 − 𝑐𝑓 𝑓 × 𝑖 𝑤ℎ𝑒𝑟𝑒 𝐿1 = 𝑙𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 𝑜𝑓 𝑡ℎ𝑖𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 𝑁 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠 𝑐𝑓 = 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑙𝑎𝑠𝑠 𝑝𝑟𝑒𝑐𝑒𝑑𝑖𝑛𝑔 𝑡ℎ𝑒 𝑡ℎ𝑖𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 𝑓 = 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑡ℎ𝑖𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 𝑖 = 𝑐𝑙𝑎𝑠𝑠 − 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙 𝑜𝑓 𝑡ℎ𝑖𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠
- 56. 𝑪𝒍𝒂𝒔𝒔 𝒇 𝒄𝒇 𝐵𝑒𝑙𝑜𝑤 50 12 12 50 − 60 30 42 60 − 70 65 107 70 − 80 78 185 80 − 90 80 265 90 − 100 55 320 10 − 110 45 365 110 − 120 25 390 𝐴𝑏𝑜𝑣𝑒 120 10 400 𝑁 = 400 𝐼𝑑𝑒𝑛𝑡𝑖𝑓𝑦𝑖𝑛𝑔 𝑡ℎ𝑒 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠: 𝑁 2 = 400 2 = 200 𝑀𝑒𝑑𝑖𝑎𝑛 𝑙𝑖𝑒𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑤𝑖𝑡ℎ 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 𝑁 2 , 𝑖. 𝑒. , 200 𝑇ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 200 𝑚𝑜𝑣𝑖𝑛𝑔 𝑖𝑛 𝑎𝑠𝑐𝑒𝑛𝑑𝑖𝑛𝑔 𝑜𝑟𝑑𝑒𝑟 = 265 𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑐𝑙𝑎𝑠𝑠 = 80 − 90 ∴ 𝑚𝑒𝑑𝑖𝑎𝑛 𝑐𝑙𝑎𝑠𝑠 = 80 − 90 ∴ 𝐿1 = 80, 𝑁 = 400, 𝑐𝑓 = 185, 𝑓 = 80, 𝑖 = 10 𝑀 = 80 + 400 2 − 185 80 × 10 = 80 + 200 − 185 8 = 80 + 15 8 = 80 + 1.875 = 81.875
- 57. 𝐼𝑑𝑒𝑛𝑡𝑖𝑓𝑦𝑖𝑛𝑔 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠: 𝑁 4 = 400 4 = 100 𝐹𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑙𝑖𝑒𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑤𝑖𝑡ℎ 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 𝑁 4 , 𝑖. 𝑒. , 100 𝑇ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 100 𝑚𝑜𝑣𝑖𝑛𝑔 𝑖𝑛 𝑎𝑠𝑐𝑒𝑛𝑑𝑖𝑛𝑔 𝑜𝑟𝑑𝑒𝑟 = 107 𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑐𝑙𝑎𝑠𝑠 = 60 − 70 ∴ 𝑓𝑖𝑟𝑠𝑡 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 = 60 − 70 ∴ 𝐿1 = 60, 𝑁 = 400, 𝑐𝑓 = 42, 𝑓 = 65, 𝑖 = 10 𝑄1 = 60 + 400 4 − 42 65 × 10 = 60 + 100 − 42 65 × 10 = 60 + 58 65 × 10 = 60 + 8.9231 = 68.9231
- 58. 𝐼𝑑𝑒𝑛𝑡𝑖𝑓𝑦𝑖𝑛𝑔 𝑡ℎ𝑒 𝑡ℎ𝑖𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠: 3𝑁 4 = 3 × 400 4 = 300 𝑇ℎ𝑖𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑙𝑖𝑒𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑙𝑎𝑠𝑠 𝑤𝑖𝑡ℎ 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 3𝑁 4 , 𝑖. 𝑒. , 300 𝑇ℎ𝑒 𝑓𝑖𝑟𝑠𝑡 𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑔𝑟𝑒𝑎𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 300 𝑚𝑜𝑣𝑖𝑛𝑔 𝑖𝑛 𝑎𝑠𝑐𝑒𝑛𝑑𝑖𝑛𝑔 𝑜𝑟𝑑𝑒𝑟 = 320 𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑐𝑙𝑎𝑠𝑠 = 90 − 100 ∴ 𝑡ℎ𝑖𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠 = 90 − 100 ∴ 𝐿1 = 90, 𝑁 = 400, 𝑐𝑓 = 265, 𝑓 = 55, 𝑖 = 10 𝑄3 = 90 + 3 × 400 4 − 265 55 × 10 = 90 + 300 − 265 55 × 10 = 90 + 35 55 × 10 = 90 + 6.3636 = 96.3636
- 59. 𝑗B = 𝑄3 + 𝑄1 − 2𝑀 𝑄3 − 𝑄1 = 96.3636 + 68.9231 − 2 × 81.875 96.3636 − 68.9231 = 165.2867 − 163.75 27.4405 = 1.5367 27.4405 = 0.056
- 60. Find the measure of skewness and kurtosis on the basis of moments for the following distribution: (2010) Marks: 5-15 15-25 25-35 35-45 45-55 No. of Students: 1 3 5 7 4
- 61. 𝐶𝑜𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡 𝑜𝑓 𝑠𝑘𝑒𝑤𝑛𝑒𝑠𝑠 𝑜𝑛 𝑡ℎ𝑒 𝑏𝑎𝑠𝑖𝑠 𝑜𝑓 𝑚𝑜𝑚𝑒𝑛𝑡𝑠, 𝛾1 = 𝜇3 𝜇2 3 2 𝜇2 = Σ𝑓𝑑 𝑥 2 𝑁 𝜇3 = Σ𝑓𝑑 𝑥 3 𝑁 ∴ 𝛾1 = Σ𝑓𝑑 𝑥 3 𝑁 Σ𝑓𝑑 𝑥 2 𝑁 3 2 = Σ𝑓𝑑 𝑥 3 𝑁 Σ𝑓𝑑 𝑥 2 𝑁 3 ∴ 𝑀𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑠𝑘𝑒𝑤𝑛𝑒𝑠𝑠: 𝛾1 = Σ𝑓𝑑 𝑥 3 𝑁 Σ𝑓𝑑 𝑥 2 3
- 62. 𝑀𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑘𝑢𝑟𝑡𝑜𝑠𝑖𝑠 𝑜𝑛 𝑡ℎ𝑒 𝑏𝑎𝑠𝑖𝑠 𝑜𝑓 𝑚𝑜𝑚𝑒𝑛𝑡𝑠, 𝛾2 = 𝜇4 𝜇2 2 − 3 𝜇2 = Σ𝑓𝑑 𝑥 2 𝑁 𝜇4 = Σ𝑓𝑑 𝑥 4 𝑁 ∴ 𝛾2 = Σ𝑓𝑑 𝑥 4 𝑁 Σ𝑓𝑑 𝑥 2 𝑁 2 − 3 ∴ 𝑀𝑒𝑎𝑠𝑢𝑟𝑒 𝑜𝑓 𝑘𝑢𝑟𝑡𝑜𝑠𝑖𝑠: 𝛾2 = 𝑁Σ𝑓𝑑 𝑥 4 Σ𝑓𝑑 𝑥 2 2 − 3
- 63. 𝐶𝑙𝑎𝑠𝑠 𝑓 𝑋 𝑓𝑥 5 − 15 1 10 10 15 − 25 3 20 60 25 − 35 5 30 150 35 − 45 7 40 280 45 − 55 4 50 200 𝑁 = 20 Σ𝑓𝑥 = 700 𝑀𝑒𝑎𝑛, 𝑋 = Σ𝑓𝑋 𝑁 = 700 20 = 35
- 64. 𝑋 𝑓 𝑑 𝑥 𝑑 𝑥 2 𝑑 𝑥 3 𝑑 𝑥 4 𝑓𝑑 𝑥 2 𝑓𝑑 𝑥 3 𝑓𝑑 𝑥 4 10 1 −25 625 −15625 390625 625 −15625 390625 20 3 −15 225 −3375 50625 675 −10125 151875 30 5 −5 25 −125 625 125 −625 3125 40 7 5 25 125 625 175 875 4375 50 4 15 225 3375 50625 900 13500 202500 𝑁 = 20 Σ𝑓𝑑 𝑥 2 = 2500 Σ𝑓𝑑 𝑥 3 = −12000 Σ𝑓𝑑 𝑥 4 = 752500 𝑆𝑘𝑒𝑤𝑛𝑒𝑠𝑠, 𝛾1 = Σ𝑓𝑑 𝑥 3 𝑁 Σ𝑓𝑑 𝑥 2 3 = −12000 × 20 2500 3 = −0.4293 ∴ 𝑡ℎ𝑒 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛 𝑖𝑠 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑒𝑙𝑦 𝑠𝑘𝑒𝑤 (𝑠𝑘𝑒𝑤 𝑡𝑜𝑤𝑎𝑟𝑑𝑠 𝑙𝑒𝑓𝑡) 𝐾𝑢𝑟𝑡𝑜𝑠𝑖𝑠, 𝛾2 = 𝑁Σ𝑓𝑑 𝑥 4 Σ𝑓𝑑 𝑥 2 2 − 3 = 20 × 752500 2500 2 − 3 = −0.592 ∴ 𝑡ℎ𝑒 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛 𝑖𝑠 𝑝𝑙𝑎𝑡𝑦𝑘𝑢𝑟𝑡𝑖𝑐 (𝑓𝑙𝑎𝑡𝑡𝑒𝑟 𝑡ℎ𝑎𝑛 𝑎 𝑛𝑜𝑟𝑚𝑎𝑙 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛)