Descriptive statistics

Descriptive
Statistics
By:-
Anand Thokal
Bhanu Chander Reddy
E. Ananta Krishna

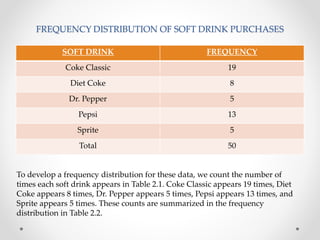
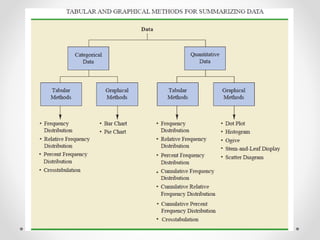
1. Summarizing Categorical Data
• FREQUENCY DISTRIBUTION:- A frequency distribution is a tabular
summary of data showing the number (frequency) of items in each
of several non overlapping classes.
• Coke Classic, Diet Coke, Dr. Pepper, Pepsi, and Sprite are five
popular soft drinks. Assume that the data in Table 2.1 show the soft
drink selected in a sample of 50 soft drink purchases.

FREQUENCY DISTRIBUTION OF SOFT DRINK PURCHASES
SOFT DRINK FREQUENCY
Coke Classic 19
Diet Coke 8
Dr. Pepper 5
Pepsi 13
Sprite 5
Total 50
To develop a frequency distribution for these data, we count the number of
times each soft drink appears in Table 2.1. Coke Classic appears 19 times, Diet
Coke appears 8 times, Dr. Pepper appears 5 times, Pepsi appears 13 times, and
Sprite appears 5 times. These counts are summarized in the frequency
distribution in Table 2.2.

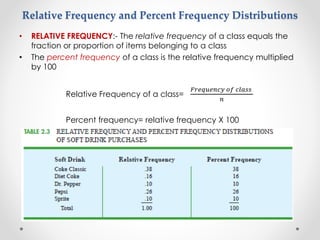
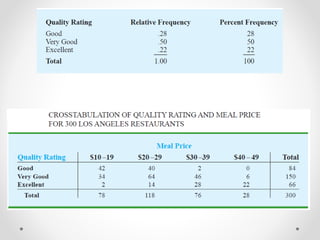
Relative Frequency and Percent Frequency Distributions
• RELATIVE FREQUENCY:- The relative frequency of a class equals the
fraction or proportion of items belonging to a class
• The percent frequency of a class is the relative frequency multiplied
by 100
Relative Frequency of a class=
𝐹𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 𝑜𝑓 𝑐𝑙𝑎𝑠𝑠
𝑛
Percent frequency= relative frequency X 100

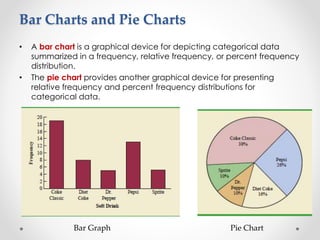
Bar Charts and Pie Charts
• A bar chart is a graphical device for depicting categorical data
summarized in a frequency, relative frequency, or percent frequency
distribution.
• The pie chart provides another graphical device for presenting
relative frequency and percent frequency distributions for
categorical data.
Bar Graph Pie Chart

2. Summarizing Quantitative Data
• Frequency Distribution’s definition holds for quantitative as well as
categorical data. However, with quantitative data we must be more
careful in defining the non overlapping classes to be used in the
frequency distribution
• For example, consider the quantitative data in Table 2.4. These data
show the time in days required to complete year-end audits for a
sample of 20 clients of Sanderson and Clifford, a small public
accounting firm. The three steps necessary to define the classes for a
frequency distribution with quantitative data are
1. Determine the number of non overlapping classes.
2. Determine the width of each class.
3. Determine the class limits. (2.4) Year-end audit time
in days
12 14 19 18
15 15 18 17
20 27 22 23
22 21 33 28
14 18 16 13

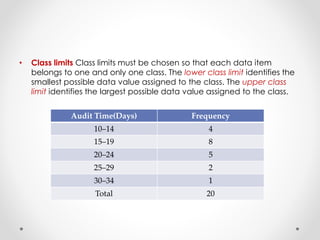
• Class limits Class limits must be chosen so that each data item
belongs to one and only one class. The lower class limit identifies the
smallest possible data value assigned to the class. The upper class
limit identifies the largest possible data value assigned to the class.
Audit Time(Days) Frequency
10–14 4
15–19 8
20–24 5
25–29 2
30–34 1
Total 20

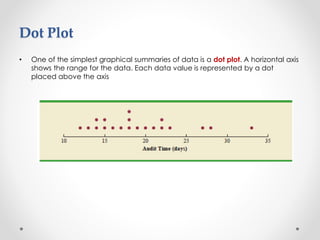
Dot Plot
• One of the simplest graphical summaries of data is a dot plot. A horizontal axis
shows the range for the data. Each data value is represented by a dot
placed above the axis

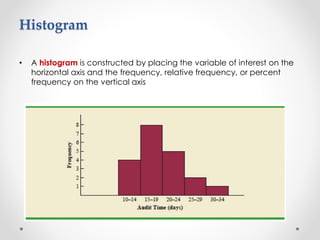
• A histogram is constructed by placing the variable of interest on the
horizontal axis and the frequency, relative frequency, or percent
frequency on the vertical axis
Histogram

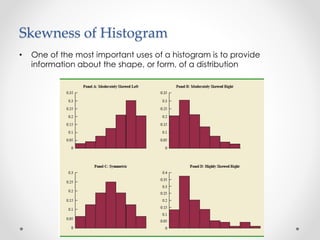
Skewness of Histogram
• One of the most important uses of a histogram is to provide
information about the shape, or form, of a distribution

Cumulative Distributions
• The cumulative frequency distribution shows the number of data
items with values less than or equal to the upper class limit of each
class
• We note that a cumulative relative frequency distribution shows the
proportion of data items, and a cumulative percent frequency
distribution shows the percentage of data items with values less than
or equal to the upper limit of each class.

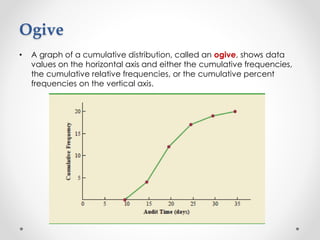
Ogive
• A graph of a cumulative distribution, called an ogive, shows data
values on the horizontal axis and either the cumulative frequencies,
the cumulative relative frequencies, or the cumulative percent
frequencies on the vertical axis.

3. Exploratory Data Analysis: The Stem-
and-Leaf Display
• The techniques of exploratory data analysis consist of simple
arithmetic and easy-to-draw graphs that can be used to summarize
data quickly. One technique—referred to as a stem-and-leaf
display—can be used to show both the rank order and shape of a
data set simultaneously.
NUMBER OF QUESTIONS ANSWERED CORRECTLY ON AN APTITUDE TEST

• Although the stem-and-leaf display may appear to offer the
same information as a histogram, it has two primary
advantages:
1. The stem-and-leaf display is easier to construct by hand.
2. Within a class interval, the stem-and-leaf display provides
more information than the histogram because the stem-and-
leaf shows the actual data.

Cross tabulations and Scatter Diagrams
• Thus far in this chapter, we have focused on tabular and graphical
methods used to summarize the data for one variable at a time.
Often a manager or decision maker requires tabular and graphical
methods that will assist in the understanding of the relationship
between two variables. Cross tabulation and scatter diagrams are
two such methods.
• Cross tabulation:- A cross tabulation is a tabular summary of data for
two variables

Scatter Diagram and Trendline
• A scatter diagram is a graphical presentation of the relationship
between two quantitative variables, and a trendline is a line that
provides an approximation of the relationship.
SAMPLE DATA FOR THE STEREO AND SOUND EQUIPMENT
STORE

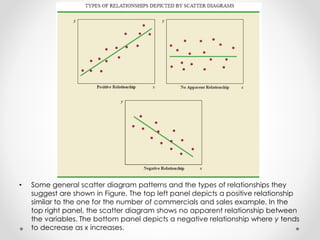
• Some general scatter diagram patterns and the types of relationships they
suggest are shown in Figure. The top left panel depicts a positive relationship
similar to the one for the number of commercials and sales example. In the
top right panel, the scatter diagram shows no apparent relationship between
the variables. The bottom panel depicts a negative relationship where y tends
to decrease as x increases.

Descriptive Statistics:
Numerical Measures

4. Measures of Location
• Mean:- Perhaps the most important measure of location is the mean,
or average value, for a variable. The mean provides a measure of
central location for the data.

• Sample mean for the given example would be:-

• Median:- The median is another measure of central location. The
median is the value in the middle when the data are arranged in
ascending order (smallest value to largest value).
• With an odd number of observations, the median is the middle value.
• An even number of observations has no single middle value so in this
case, we take average of the values for the middle two observations.

• Mode:- The mode is the value that occurs with greatest frequency.
• Percentiles:- A percentile provides information about how the data
are spread over the interval from the smallest value to the largest
value

Quartiles
• Quartiles are just specific percentiles; thus, the steps for computing percentiles
can be applied directly in the computation of quartiles.

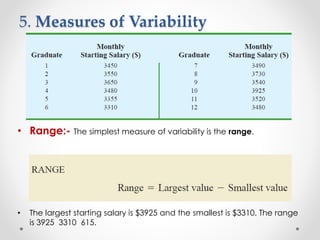
5. Measures of Variability
• Range:- The simplest measure of variability is the range.
• The largest starting salary is $3925 and the smallest is $3310. The range
is 3925 3310 615.

• Interquartile Range:-A measure of variability that overcomes the
dependency on extreme values is the interquartile range (IQR).
• Variance:- The variance is a measure of variability that utilizes all the
data.
• The difference between each xi and the mean ( for a sample, μ for a
population) is called a deviation about the mean.
• If the data are for a population, the average of the squared
deviations is called the population variance.

• Although a detailed explanation is beyond the scope of this text, it
can be shown that if the sum of the squared deviations about the
sample mean is divided by n-1, and not n, the resulting sample
variance provides an unbiased estimate of the population variance.

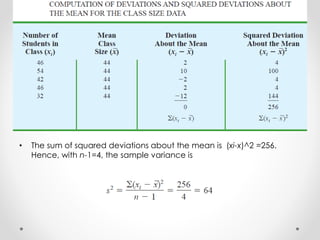
• The sum of squared deviations about the mean is (xi-x)^2 =256.
Hence, with n-1=4, the sample variance is

• Standard Deviation:- The standard deviation is defined to be the
positive square root of the variance.
• Hence the Sample Standard Deviation=8, for the latest example
• Coefficient of Variation:- In some situations we may be interested in a
descriptive statistic that indicates how large the standard deviation is
relative to the mean. This measure is called the coefficient of
variation and is usually expressed as a percentage.

• For the class size data, we found a sample mean of 44 and a sample
standard deviation of 8. The coefficient of variation is [(8/44)X100]%
=18.2%. In words, the coefficient of variation tells us that the sample
standard deviation is 18.2% of the value of the sample mean.

6. Measures of Distribution Shape, Relative
Location, and Detection of Outliers
• Distribution Shape
For a
symmetric
distribution,
the mean and
the median
are equal.

• z-Scores:- In addition to measures of location, variability, and shape,
we are also interested in the relative location of values within a data
set.
• Measures of relative location help us determine how far a particular
value is from the mean.
• By using both the mean and standard deviation, we can determine
the relative location of any observation.
• The z-score is often called the standardized value. The z-score, zi,
can be interpreted as the number of standard deviations xi is
from the mean . For example, z1=1.2 would indicate that x1 is1.2
standard deviations greater than the sample mean.

• CHEBYSHEV’S THEOREM:- At least (1 1/z 2) of the data values must be
within z standard deviations of the mean, where z is any value
greater than 1.
• Some of the implications of this theorem, with z 2, 3, and 4 standard
deviations, follo:
• At least .75, or 75%, of the data values must be within z =2 standard
deviations of the mean.

• For an example using Chebyshev’s theorem, suppose that the
midterm test scores for 100 students in a college business statistics
course had a mean of 70 and a standard deviation of 5. How many
students had test scores between 60 and 80?
• For the test scores between 60 and 80,
• We note that 60 is two standard deviations below the mean and 80 is
two standard deviations above the mean.
• Using Chebyshev’s theorem, we see that at least .75, or at least 75%,
of the observations must have values within two standard deviations
of the mean.
• Thus, at least 75% of the students must have scored between 60 and
80.

• Outliers:- Sometimes a data set will have one or more observations
with unusually large or unusually small values. These extreme values
are called outliers.

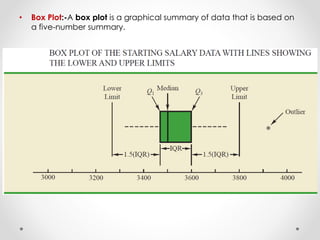
7. Exploratory Data Analysis
• Five-Number Summary:- In a five-number summary, the following five
numbers are used to summarize the data:
1. Smallest value
2. First quartile (Q1)
3. Median (Q2)
4. Third quartile (Q3)
5. Largest value
• The easiest way to develop a five-number summary is to first place
the data in ascending order. Then it is easy to identify the smallest
value, the three quartiles, and the largest value.

• Box Plot:-A box plot is a graphical summary of data that is based on
a five-number summary.

8. Measures of Association Between
Two Variables
• Covariance:-

9. The Weighted Mean and Working
with Grouped Data
• Grouped Data:- In most cases, measures of location and
variability are computed by using the individual data values.
Sometimes, however, data are available only in a grouped or
frequency distribution form. In the following discussion, we
show how the weighted mean formula can be used to obtain
approximations of the mean, variance, and standard
deviation for grouped data.

Descriptive statistics

More Related Content

What's hot (20)

Similar to Descriptive statistics (20)

More from Anand Thokal (10)

Recently uploaded (20)

Descriptive statistics