Descriptive statistics

DESCRIPTIVE STATISTICSDESCRIPTIVE STATISTICS
Dr Htin Zaw SoeDr Htin Zaw Soe
MBBS, DFT, MMedSc (P & TM), PhD, DipMedEdMBBS, DFT, MMedSc (P & TM), PhD, DipMedEd
Associate ProfessorAssociate Professor
Department of BiostatisticsDepartment of Biostatistics
University of Public HealthUniversity of Public Health

 Raw dataRaw data::
Measurements which have not been organized, summarized, orMeasurements which have not been organized, summarized, or
otherwise manipulatedotherwise manipulated
 Descriptive measuresDescriptive measures::
Single numbers calculated from organized and summarizedSingle numbers calculated from organized and summarized
data to describe these data. eg. Percentage, averagedata to describe these data. eg. Percentage, average

I. The Ordered ArrayI. The Ordered Array
 First step in organizing data is the preparation of anFirst step in organizing data is the preparation of an orderedordered
arrayarray..
 An ordered array – listing of the values of a collection (eitherAn ordered array – listing of the values of a collection (either
population or sample) in order of magnitude from the smallestpopulation or sample) in order of magnitude from the smallest
value to the largest valuevalue to the largest value
eg. 12, 3, 15, 21, 8, 9, 17, 13, 22, 4, 12, 10 →eg. 12, 3, 15, 21, 8, 9, 17, 13, 22, 4, 12, 10 →
3, 4, 8, 9, 10, 12, 12, 13, 15, 17, 21, 223, 4, 8, 9, 10, 12, 12, 13, 15, 17, 21, 22

II. Grouped Data – The Frequency DistributionII. Grouped Data – The Frequency Distribution
 Data grouping → data summarization → informationData grouping → data summarization → information
 To group data (a set of observations),To group data (a set of observations), class intervalsclass intervals areare
neededneeded
 Too few class interval →loss of informationToo few class interval →loss of information
 Too many class interval → loss of objective of summarizationToo many class interval → loss of objective of summarization
 Rule of thumb: In the range ofRule of thumb: In the range of sixsix toto fifteenfifteen class intervalsclass intervals

 To calculate requiredTo calculate required number of class intervalnumber of class interval for a set offor a set of
data →data → Sturges’s FormulaSturges’s Formula
 number of class interval =number of class interval = k = 1 + 3.322 (logk = 1 + 3.322 (log1010 nn))
 Width of class interval (Width of class interval (ww):): ww == RR // kk
((RR = Range of data)= Range of data)
 Width of class interval → 5 units, 10 units (multiples of 10)Width of class interval → 5 units, 10 units (multiples of 10)

 ExampleExample: We want to know how many class interval and how: We want to know how many class interval and how
wide the interval in a following data set of ages ofwide the interval in a following data set of ages of 189189 studystudy
subjectssubjects
30,30, 34, 35, 37, 38, 38, ………………76, 77, 78, 78, 78,34, 35, 37, 38, 38, ………………76, 77, 78, 78, 78, 8282
k = 1 + 3.322 (logk = 1 + 3.322 (log1010 nn))
= 1 + 3.322 (log= 1 + 3.322 (log1010 189)189)
= 1 + 3.322 (2.2764618)= 1 + 3.322 (2.2764618)
≈≈ 99
ww == RR // kk
= (82 – 30) / 9= (82 – 30) / 9
= 5.778= 5.778
5 or 10 is more convenient to use as a class interval5 or 10 is more convenient to use as a class interval

 Supposing 10 is used, construct the intervals as follow.Supposing 10 is used, construct the intervals as follow.
30 – 3930 – 39
40 – 4940 – 49
50 – 5950 – 59
60 – 6960 – 69
70 – 7970 – 79
80 – 8980 – 89

 Supposing 5 is used, construct the intervals as follow.Supposing 5 is used, construct the intervals as follow.
30 – 3430 – 34
35 – 3935 – 39
40 – 4440 – 44
45 – 4945 – 49
50 – 5450 – 54
55 – 5955 – 59
60 – 6460 – 64
65 – 6965 – 69
70 – 7470 – 74
75 – 7975 – 79
80 – 8480 – 84

 Midpoint of a class intervalMidpoint of a class interval = sum of upper and lower limits of= sum of upper and lower limits of
interval divided by 2interval divided by 2
eg. Midpoint of a class interval = 30 + 39 / 2 = 34.5eg. Midpoint of a class interval = 30 + 39 / 2 = 34.5
 Frequency distributionFrequency distribution
 Relative frequencyRelative frequency
 Cumulative FrequencyCumulative Frequency
 Cumulative Relative FrequencyCumulative Relative Frequency

Table 1. Frequency, Cumulative Frequency, Relative Frequency,Table 1. Frequency, Cumulative Frequency, Relative Frequency,
Cumulative Relative Frequency Distributions of Ages of 189Cumulative Relative Frequency Distributions of Ages of 189
SubjectsSubjects
Class intervalClass interval FrequencyFrequency CumulativeCumulative
FrequencyFrequency
RelativeRelative
FrequencyFrequency
CumulativeCumulative
RelativeRelative
FrequencyFrequency
30 – 3930 – 39
40 – 4940 – 49
50 – 5950 – 59
60 – 6960 – 69
70 – 7970 – 79
80 – 8980 – 89
1111
4646
7070
4545
1616
11
1111
5757
127127
172172
188188
189189
.0582.0582
.2434.2434
.3704.3704
.2381.2381
.0847.0847
.0053.0053
.0582.0582
.3016.3016
.6720.6720
.9101.9101
.9948.9948
1.00011.0001
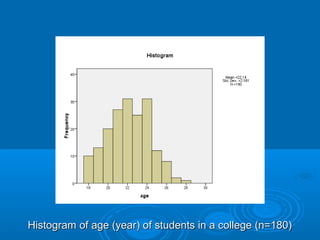
TotalTotal 189189 1.00011.0001

 Use of 'cumulative' is:Use of 'cumulative' is:
If we want to know frequency between 50-59 and 70- 79, weIf we want to know frequency between 50-59 and 70- 79, we
subtract 57 from 188 (ie 188 – 57 = 131)subtract 57 from 188 (ie 188 – 57 = 131)
 HistogramHistogram : A special type of bar graph showing frequency: A special type of bar graph showing frequency
distribution (See Figure)distribution (See Figure)
 True class limit is used for continuity of values or observationsTrue class limit is used for continuity of values or observations

Histogram of age (year) of students in a college (n=180)Histogram of age (year) of students in a college (n=180)

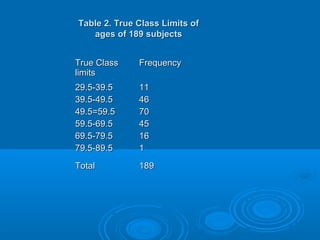
Table 2. True Class Limits ofTable 2. True Class Limits of
ages of 189 subjectsages of 189 subjects
True ClassTrue Class
limitslimits
FrequencyFrequency
29.5-39.529.5-39.5
39.5-49.539.5-49.5
49.5=59.549.5=59.5
59.5-69.559.5-69.5
69.5-79.569.5-79.5
79.5-89.579.5-89.5
1111
4646
7070
4545
1616
11
TotalTotal 189189

 Frequency PolygonFrequency Polygon: a special kind of line graph connecting: a special kind of line graph connecting
midpoints at the tops of bars or cells of histogrammidpoints at the tops of bars or cells of histogram
Total area under the frequency polygon is equal to that ofTotal area under the frequency polygon is equal to that of
histogram (See Figure)histogram (See Figure)
 Stem-and-Leaf DisplaysStem-and-Leaf Displays: It resembles with histogram and: It resembles with histogram and
serves the same purpose (range of data set, location of highestserves the same purpose (range of data set, location of highest
concentration of measurements, presence or absence ofconcentration of measurements, presence or absence of
symmetry)symmetry)
Two advantages over histogram: (a) preserve individual'sTwo advantages over histogram: (a) preserve individual's
measurementsmeasurements
: (b) ordered array step is not: (b) ordered array step is not
necessary as tallying processnecessary as tallying process
presentpresent

 Example: Construct a stem-and-leaf display using the followingExample: Construct a stem-and-leaf display using the following
observations (ages) of 30 subjectsobservations (ages) of 30 subjects
35 3235 32 2121 43 39 6043 39 60
3636 1212 54 45 37 5354 45 37 53
4545 2323 6464 1010 3434 2222
36 45 55 44 55 4636 45 55 44 55 46
2222 38 35 56 45 5738 35 56 45 57
11 0202
22 12231223
3 2455667893 245566789
4 34555564 3455556
5 3455675 345567
6 046 04

III. Measures of Central TendencyIII. Measures of Central Tendency
 StatisticStatistic : A descriptive measure computed from the data of a: A descriptive measure computed from the data of a
samplesample
 ParameterParameter : A descriptive measure computed from the data of: A descriptive measure computed from the data of
a populationa population
 Most commonly used measures of central tendency:Most commonly used measures of central tendency:
Mean, Median, ModeMean, Median, Mode

 Mean or Arithmetic MeanMean or Arithmetic Mean: also called 'Average': also called 'Average'
: obtained by adding all the values: obtained by adding all the values
in a population or a sample and dividing by the number ofin a population or a sample and dividing by the number of
values that are addedvalues that are added
Formula of the mean: For a finite population:Formula of the mean: For a finite population: μ = ∑ xμ = ∑ xii / N/ N
: For a sample :: For a sample : x = ∑ xx = ∑ xii / n/ n
Eg. Mean age (year) of the following 9Eg. Mean age (year) of the following 9
subjectssubjects
56, 54, 61, 60, 54, 44, 49, 50, 6356, 54, 61, 60, 54, 44, 49, 50, 63
x = ∑ xx = ∑ xii / n/ n
= 56+54+61+60+54+44+49+50+63 / 9= 56+54+61+60+54+44+49+50+63 / 9
= 54.55 year= 54.55 year

 Geometric meanGeometric mean:: used in skewed data setused in skewed data set
Steps: Take logarithm (to base 10 or base e) of each valueSteps: Take logarithm (to base 10 or base e) of each value
: Find the (arithmetic) mean of the log transformed: Find the (arithmetic) mean of the log transformed
valuesvalues
: Take antilog of the obtained mean: Take antilog of the obtained mean
Weighted meanWeighted mean: used if the variable of interest is regarded: used if the variable of interest is regarded
more important than othersmore important than others
ww11xx11 +w+w22xx22+…w+…wnnxxnn // ww11+w+w22+…w+…wnn == ∑ w∑ wii xxii / ∑ w/ ∑ wii
 Properties of the mean:Properties of the mean:

UniquenessUniqueness

SimplicitySimplicity

Being influenced by extreme valuesBeing influenced by extreme values

 MedianMedian:: Middle value in a set of dataMiddle value in a set of data
If number of value is odd, median is the middle valueIf number of value is odd, median is the middle value
If number of value is even, median is average of twoIf number of value is even, median is average of two
middle valuesmiddle values
Formula:Formula: ( n + 1) / 2th value( n + 1) / 2th value
eg. Median age (year) of the following 9 subjectseg. Median age (year) of the following 9 subjects
56, 54, 61, 60, 54, 44, 49, 50, 6356, 54, 61, 60, 54, 44, 49, 50, 63
Ordered array → 44, 49, 50, 54, 54, 56, 60, 61, 63Ordered array → 44, 49, 50, 54, 54, 56, 60, 61, 63
( n + 1) / 2th value( n + 1) / 2th value → (9 + 1) /2 = 10/ 2 = 5th value→ (9 + 1) /2 = 10/ 2 = 5th value
5th value is 54, so median is 545th value is 54, so median is 54

 Properties of MedianProperties of Median::
- Uniqueness- Uniqueness
- Simplicity- Simplicity
- Not Being as drastically affected by extreme values as in- Not Being as drastically affected by extreme values as in
medianmedian

 The ModeThe Mode: Value most frequently occurring in a set of data: Value most frequently occurring in a set of data
: More than one mode present: More than one mode present
eg. Modal age (year) of the following 9 subjectseg. Modal age (year) of the following 9 subjects
56,56, 5454, 61, 60,, 61, 60, 5454, 44, 49, 50, 63, 44, 49, 50, 63
54 is modal age54 is modal age
The mode is used to describe the qualitative data (eg. medicalThe mode is used to describe the qualitative data (eg. medical
diagnosis)diagnosis)

IV. Measures of dispersionIV. Measures of dispersion
Dispersion: synonyms → variation, spread, scatterDispersion: synonyms → variation, spread, scatter
 The RangeThe Range: The difference between the largest and smallest: The difference between the largest and smallest
value in a set of datavalue in a set of data
:: R = xR = xLL - x- xSS
eg. The range of ages (year) of the following 9 subjectseg. The range of ages (year) of the following 9 subjects
56, 54, 61, 60, 54,56, 54, 61, 60, 54, 4444, 49, 50,, 49, 50, 6363
R = xR = xLL
- x- xSS = 63 – 44 = 19= 63 – 44 = 19
The usefulness of the range is limited; simplicity of itsThe usefulness of the range is limited; simplicity of its
computation presentcomputation present

 The VarianceThe Variance: It shows scatter of the values about their mean: It shows scatter of the values about their mean
in a set of data.in a set of data.
Sample variance =Sample variance = ss22
= ∑ ( x= ∑ ( xii – x)– x)22
/ n – 1/ n – 1
Finite population variance =Finite population variance = σσ22
= ∑ ( x= ∑ ( xii – μ)– μ)22
/ N/ N ;;
(not N – 1)(not N – 1)
 Degree of freedomDegree of freedom::
The sum of deviations of the values from their mean is equal toThe sum of deviations of the values from their mean is equal to
zerozero
If we know values ofIf we know values of n – 1n – 1 of deviation from their mean, nth one isof deviation from their mean, nth one is
automatically determinedautomatically determined
(Number of independent pieces of information available for the(Number of independent pieces of information available for the
statistician to make the calculations)statistician to make the calculations)

 Standard deviationStandard deviation:: √ s√ s22
(For a sample)(For a sample)
:: √ σ√ σ22
(For a population)(For a population)
 Coefficient of Variation (CV)Coefficient of Variation (CV) : Standard deviation as a: Standard deviation as a
percentage of the meanpercentage of the mean
(Relative variation, not(Relative variation, not
absolute variation)absolute variation)
:: CV = (s / x) (100)CV = (s / x) (100)
 CV is used to compare the dispersions in two sets of data in theCV is used to compare the dispersions in two sets of data in the
conditions of:conditions of:
1 . Different units of measurement in different variables1 . Different units of measurement in different variables
[eg Cholesterol level (mg per 100 ml) vs Body weight of adult[eg Cholesterol level (mg per 100 ml) vs Body weight of adult
(lb) ](lb) ]

2. Same units of measurement in same variables but different2. Same units of measurement in same variables but different
entitiesentities
[eg. Body weight (lb) of adult vs Body weight (lb) of children][eg. Body weight (lb) of adult vs Body weight (lb) of children]
eg.eg. Adult ChildrenAdult Children
Mean weight (x) (lb) 145 lb 80 lbMean weight (x) (lb) 145 lb 80 lb
SD (s) 10 lb 10 lbSD (s) 10 lb 10 lb
Adult’s CV = (s / x) (100) = (10/ 145) (100) = 6.9Adult’s CV = (s / x) (100) = (10/ 145) (100) = 6.9
Children’s CV = (s / x) (100) = (10/ 80) (100) = 12.5Children’s CV = (s / x) (100) = (10/ 80) (100) = 12.5
Variation is much higher in children than in adultsVariation is much higher in children than in adults

3. Different units of measurement in same variables (Body3. Different units of measurement in same variables (Body
weights – lb vs Kg)weights – lb vs Kg)
4. Comparing results obtained by different persons investigating4. Comparing results obtained by different persons investigating
the same variablethe same variable
 Percentiles and QuartilesPercentiles and Quartiles::
 PercentilesPercentiles ::
Given a set ofGiven a set of nn observation xobservation x11, x, x22, …x, …xnn, the, the ppth percentileth percentile PP isis
the value ofthe value of XX such thatsuch that pp percent or less of the observationspercent or less of the observations
are less thanare less than PP and (100-and (100- pp) percent or less of the observations) percent or less of the observations
are greater thanare greater than PP

10th percentile ,10th percentile , PP1010
50th percentile,50th percentile, PP5050, Median, Median
25th percentile,25th percentile, PP2525, First quartile, Q, First quartile, Q11
50th percentile,50th percentile, PP5050, Second quartile, Q, Second quartile, Q22 ((MedianMedian))
75th percentile,75th percentile, PP7575, Third quartile, Q, Third quartile, Q33
Formulae for QFormulae for Q11, Q, Q22 and Qand Q33
QQ11 = ( n + 1) / 4 th ordered observation= ( n + 1) / 4 th ordered observation
QQ22 = 2( n + 1) / 4 = ( n + 1) / 2 th ordered observation= 2( n + 1) / 4 = ( n + 1) / 2 th ordered observation
QQ33 = 3( n + 1) / 4 th ordered observation= 3( n + 1) / 4 th ordered observation

 Interquartile range (IQR)Interquartile range (IQR): The difference between the third: The difference between the third
and first quartilesand first quartiles
:: IQR = QIQR = Q33 – Q– Q11
-Variability among middle 50% of the observations in a-Variability among middle 50% of the observations in a
data setdata set
- The larger the IQR, the more variable the data in middle 50%- The larger the IQR, the more variable the data in middle 50%
and vice versaand vice versa
- (IQR/R) 100% - IQR of overall range in percent- (IQR/R) 100% - IQR of overall range in percent

Box-and-Whisker Plots (Boxplots)Box-and-Whisker Plots (Boxplots)
Five steps to draw boxplotsFive steps to draw boxplots
- Variable of interest on the horizontal axisVariable of interest on the horizontal axis
- Draw a box (L end – QDraw a box (L end – Q11, R end- Q, R end- Q33))
- Divide it by a vertical line – median (QDivide it by a vertical line – median (Q22))
- A whisker from L end to smallest measurementA whisker from L end to smallest measurement
- A whisker from R end to largest measurementA whisker from R end to largest measurement
 Its use: it shows – amount of spread, location of concentrationIts use: it shows – amount of spread, location of concentration
and symmetry of dataand symmetry of data
 See Example 2.5.4 (pp 46)See Example 2.5.4 (pp 46)

 Example:Example:
 Ground Reaction Forces Measurements when trotting of 20Ground Reaction Forces Measurements when trotting of 20
dogs with lame ligamentdogs with lame ligament
14.6 24.3 24.9 27.014.6 24.3 24.9 27.0 27.227.2 27.427.4 28.2 28.8 29.928.2 28.8 29.9 30.730.7
31.531.5 31.6 32.3 32.8 33.3 33.6 34.3 36.9 38.3 44.031.6 32.3 32.8 33.3 33.6 34.3 36.9 38.3 44.0
QQ11 = ( n + 1) / 4 th ordered observation= ( n + 1) / 4 th ordered observation
= (20 + 1) / 4 = 5.25 th ordered observation= (20 + 1) / 4 = 5.25 th ordered observation
= 27.2 + (27.4 - 27.2) 0.25 = 27.2 + 0.05 == 27.2 + (27.4 - 27.2) 0.25 = 27.2 + 0.05 = 27.2527.25
QQ22 = 2( n + 1) / 4 = ( n + 1) / 2 th ordered observation= 2( n + 1) / 4 = ( n + 1) / 2 th ordered observation
= (20 + 1) / 2 = 10.5 th ordered observation= (20 + 1) / 2 = 10.5 th ordered observation
= 30.7 + (31.5 – 30.7) 0.5 = 30.7 + 0.4 == 30.7 + (31.5 – 30.7) 0.5 = 30.7 + 0.4 = 31.131.1
QQ33 = 3( n + 1) / 4 th ordered observation= 3( n + 1) / 4 th ordered observation
== 33.52533.525

Descriptive statistics

More Related Content

What's hot (20)

Similar to Descriptive statistics (20)

More from Mmedsc Hahm (20)

Recently uploaded (20)

Descriptive statistics