Manpreet kay bhatia Business Statistics.ppt
- 1. „There are three kinds of lies: lies, damned lies, and statistics.“ (B.Disraeli) Introduction To Statistics
- 2. Why study statistics? 1. Data are everywhere 2. Statistical techniques are used to make many decisions that affect our lives 3. No matter what your career, you will make professional decisions that involve data. An understanding of statistical methods will help you make these decisions efectively
- 3. Applications of statistical concepts in the business world Finance – correlation and regression, index numbers, time series analysis Marketing – hypothesis testing, chi-square tests, nonparametric statistics Personel – hypothesis testing, chi-square tests, nonparametric tests Operating management – hypothesis testing, estimation, analysis of variance, time series analysis
- 4. Statistics The science of collectiong, organizing, presenting, analyzing, and interpreting data to assist in making more effective decisions Statistical analysis – used to manipulate summarize, and investigate data, so that useful decision-making information results.
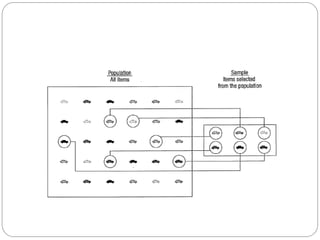
- 6. Types of statistics Descriptive statistics – Methods of organizing, summarizing, and presenting data in an informative way Inferential statistics – The methods used to determine something about a population on the basis of a sample Population –The entire set of individuals or objects of interest or the measurements obtained from all individuals or objects of interest Sample – A portion, or part, of the population of interest
- 8. Inferential Statistics Estimation e.g., Estimate the population mean weight using the sample mean weight Hypothesis testing e.g., Test the claim that the population mean weight is 70 kg Inference is the process of drawing conclusions or making decisions about a population based on sample results
- 9. Sampling a sample should have the same characteristics as the population it is representing. Sampling can be: with replacement: a member of the population may be chosen more than once (picking the candy from the bowl) without replacement: a member of the population may be chosen only once (lottery ticket)
- 10. Sampling methods Sampling methods can be: random (each member of the population has an equal chance of being selected) nonrandom The actual process of sampling causes sampling errors. For example, the sample may not be large enough or representative of the population. Factors not related to the sampling process cause nonsampling errors. A defective counting device can cause a nonsampling error.
- 11. Random sampling methods simple random sample (each sample of the same size has an equal chance of being selected) stratified sample (divide the population into groups called strata and then take a sample from each stratum) cluster sample (divide the population into strata and then randomly select some of the strata. All the members from these strata are in the cluster sample.) systematic sample (randomly select a starting point and take every n-th piece of data from a listing of the population)
- 12. Descriptive Statistics Collect data e.g., Survey Present data e.g., Tables and graphs Summarize data e.g., Sample mean = i X n
- 13. Statistical data The collection of data that are relevant to the problem being studied is commonly the most difficult, expensive, and time- consuming part of the entire research project. Statistical data are usually obtained by counting or measuring items. Primary data are collected specifically for the analysis desired Secondary data have already been compiled and are available for statistical analysis A variable is an item of interest that can take on many different numerical values. A constant has a fixed numerical value.
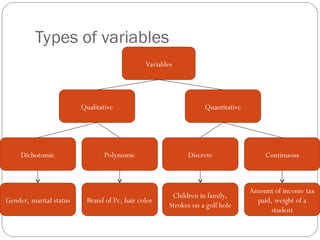
- 14. Data Statistical data are usually obtained by counting or measuring items. Most data can be put into the following categories: Qualitative - data are measurements that each fail into one of several categories. (hair color, ethnic groups and other attributes of the population) quantitative - data are observations that are measured on a numerical scale (distance traveled to college, number of children in a family, etc.)
- 15. Qualitative data Qualitative data are generally described by words or letters. They are not as widely used as quantitative data because many numerical techniques do not apply to the qualitative data. For example, it does not make sense to find an average hair color or blood type. Qualitative data can be separated into two subgroups: dichotomic (if it takes the form of a word with two options (gender - male or female) polynomic (if it takes the form of a word with more than two options (education - primary school, secondary school and university).
- 16. Quantitative data Quantitative data are always numbers and are the result of counting or measuring attributes of a population. Quantitative data can be separated into two subgroups: discrete (if it is the result of counting (the number of students of a given ethnic group in a class, the number of books on a shelf, ...) continuous (if it is the result of measuring (distance traveled, weight of luggage, …)
- 17. Types of variables Variables Quantitative Qualitative Dichotomic Polynomic Discrete Continuous Gender, marital status Brand of Pc, hair color Children in family, Strokes on a golf hole Amount of income tax paid, weight of a student
- 18. Numerical scale of measurement: Nominal – consist of categories in each of which the number of respective observations is recorded. The categories are in no logical order and have no particular relationship. The categories are said to be mutually exclusive since an individual, object, or measurement can be included in only one of them. Ordinal – contain more information. Consists of distinct categories in which order is implied. Values in one category are larger or smaller than values in other categories (e.g. rating-excelent, good, fair, poor) Interval – is a set of numerical measurements in which the distance between numbers is of a known, sonstant size. Ratio – consists of numerical measurements where the distance between numbers is of a known, constant size, in addition, there is a nonarbitrary zero point.
- 20. Data presentation „ The question is“ said Alice, „whether you can make words mean so many different things.“ „The question is,“ said Humpty Dumpty, „which is to be master-that´s all.“ (Lewis Carroll)
- 21. Numerical presentation of qualitative data pivot table (qualitative dichotomic statistical attributes) contingency table (qualitative statistical attributes from which at least one of them is polynomic) You should know how to convert absolute values to relative ones (%).
- 22. Frequency distributions – numerical presentation of quantitative data Frequency distribution – shows the frequency, or number of occurences, in each of several categories. Frequency distributions are used to summarize large volumes of data values. When the raw data are measured on a qunatitative scale, either interval or ration, categories or classes must be designed for the data values before a frequency distribution can be formulated.
- 23. Steps for constructing a frequency distribution 1. Determine the number of classes 2. Determine the size of each class 3. Determine the starting point for the first class 4. Tally the number of values that occur in each class 5. Prepare a table of the distribution using actual counts and/ or percentages (relative frequencies) m n max min h m
- 24. Frequency table absolute frequency “ni” (Data TabData AnalysisHistogram) relative frequency “fi” Cumulative frequency distribution shows the total number of occurrences that lie above or below certain key values. cumulative frequency “Ni” cumulative relative frequency “Fi”
- 25. Charts and graphs Frequency distributions are good ways to present the essential aspects of data collections in concise and understable terms Pictures are always more effective in displaying large data collections
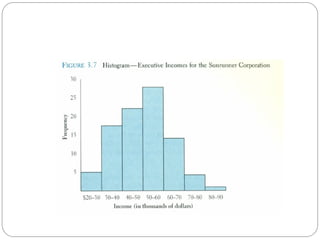
- 26. Histogram Frequently used to graphically present interval and ratio data Is often used for interval and ratio data The adjacent bars indicate that a numerical range is being summarized by indicating the frequencies in arbitrarily chosen classes
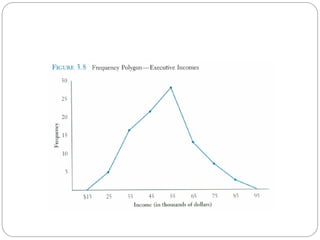
- 28. Frequency polygon Another common method for graphically presenting interval and ratio data To construct a frequency polygon mark the frequencies on the vertical axis and the values of the variable being measured on the horizontal axis, as with the histogram. If the purpose of presenting is comparation with other distributions, the frequency polygon provides a good summary of the data
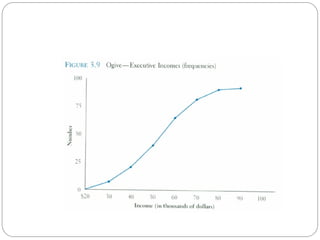
- 30. Ogive A graph of a cumulative frequency distribution Ogive is used when one wants to determine how many observations lie above or below a certain value in a distribution. First cumulative frequency distribution is constructed Cumulative frequencies are plotted at the upper class limit of each category Ogive can also be constructed for a relative frequency distribution.
- 32. Pie Chart The pie chart is an effective way of displaying the percentage breakdown of data by category. Useful if the relative sizes of the data components are to be emphasized Pie charts also provide an effective way of presenting ratio- or interval-scaled data after they have been organized into categories