Measurement and descriptive statistics

G R O U P 1 :
N G U Y Ễ N T R Ầ N H O À I P H Ư Ơ N G
P H Ạ M P H Ú C K H Á N H M I N H
N G U Y Ễ N N G Ọ C C H Â U
N G U Y Ễ N M Ỹ K H Á N H
V Õ T H Ị T H A N H T H Ư
Đ Ỗ T H Ị B Ạ C H V Â N
CHAPTER 3
Measurement and Descriptive Statistics

Outline
3.1. Frequency distributions
3.2. Levels of measurement
3.2.1. Nominal
3.2.2. Ordinal
3.2.3. Interval
3.2.4. Ratio
3.3. Descriptive Statistics and Plots
3.3.1. Frequency tables
3.3.2. Bar charts
3.3.3. Histograms
3.3.4. Frequency Polygons
3.3.5. Box and Whiskers Plot
3.3.6. Measures of Central Tendency
3.3.7. Measures of Variability
3.3.8. Standard Deviation
3.3.9. Interquartile range
3.3.10.Measurement and Descriptive Statistics

3.1. Frequency Distributions
A frequency distribution is a tally or count of the
number of times each score on a single variable
occurs.
Grade Frequency
A 7
B 20
C 18
D 5
Total 50
Example:

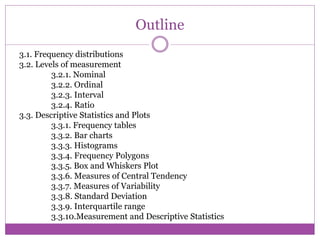
Approximately normal distribution
 The largest number of students has scores between 450
and 550 (the middle two bars).
 Small numbers of students have very low and very high
scores.

Approximately normal distribution
 When there are most scores for the middle values and a
small number of scores for the low and high values, the
distribution is said to be approximately normal.
normal,
bell
shaped
curve

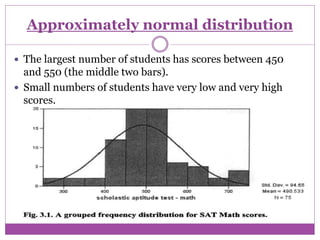
Non-normal distribution
 The tail of the curve is on the low end or left side.
 This distribution can be said to be NOT normally
distributed.
different
from
normal
curve

3.2. Levels of measurement
Nominal
Ordinal
Interval
Ratio

3.2.1. Nominal
 Two or more unordered categories
Example:

3.2.2. Ordinal
 Ordered levels, in which the difference
in magnitude between levels is not
equal.
Example:
very dissatisfied
somewhat dissatisfied
somewhat satisfied
1
2
3
4 very satisfied

3.2.3. Interval
 Ordered levels, in which the difference in magnitude
between levels is equal
 Example: Temperature, Dates (data that has an
arbitrary zero), etc.

3.2.4. Ratio
 Interval data with a natural zero point (data that has
an absolute zero)
Example: height, weight, age, length, ruler, year of
experience, etc.

Identify the scale of measurement for the
following: military title -- Lieutenant,
Captain, Major.
A. nominal
B. ordinal
C. interval
D. ratio
Question 1

Question 2
following categorization of clothing: hat, shirt,
shoes, pants
A. nominal
B. ordinal
C. interval
D. ratio

Question 3
following: heat measured in degrees
centigrade.
A. nominal
B. ordinal
C. interval
D. ratio

Question 4
A score on a 5-point quiz measuring knowledge
of algebra is an example of a(n)
A. nominal
B. ordinal
C. interval
D. ratio

Question 5
Amount of money you have in your pocket
right now (25 cents, 55 cents, etc.) is an
example of:
A. nominal
B. ordinal
C. interval
D. ratio

3.3. Descriptive Statistics and Plots
Frequency tables
Bar charts
Histograms
Frequency Polygons
Box and Whiskers Plot
Measures of Central Tendency
Measures of Variability
Standard Deviation
Interquartile range
Measurement and Descriptive Statistics

3.3.1. Frequency Tables
A frequency table is a table that shows the total
for each category or group of data.

3.3.2. Bar chart
Bar charts are used well for the frequency
distribution of variables like religion, ethic
group or other nominal variables.
0
5
10
15
20
25
30
35
Protestant Catholic No religion

3.3.3. Histograms
Histograms look like bar charts; however there is no
space between the boxes, indicating that there is a
continuous variable theoretically underlying the
scores.

3.3.4. Frequency Polygons
It connects the points between the categories and is
best used with approximately normal data. It is also
used with ordinal data.

3.3.5. Box and Whiskers Plot
It is a graphical representation of the distributions of scores
and is helpful in distinguishing between ordinal and normally
distributed data.

3.3.6. Measures of Central Tendency
Three measures of the center of a distribution are
commonly used: mean, median and mode.
1. Mean: sum of the values divided by the
number of cases
Example: We have a set of data: 15, 24, 49, 8, 50.
Mean: (15 +24 + 49 +8 +50)/5 = 29. 2

2. Median: the middle score or median is the
appropriate measure of central tendency for ordinal
level raw data.
The median represents the middle of the ordered
sample data
- When the sample size is even, the median is the
midpoint/mean of the two middle values

- When the sample size is odd, the median is the middle value.

3. Mode: is the number that appeared frequently
in the data set.

3.3.7. Measures of Variability
Variability tells us about the spread or dispersion of the
scores.
1. Range: the area of variation between upper and lower
limits on a particular scale.
Example: 8, 15, 24, 47, 50
=> Range = 50 – 8 = 42.

2. Standard deviation: (SD) measures the amount of
variation or dispersion from the average.
Example: 1, 2, 3, 4, 5
+ Mean: = (1 +2+3+4+5)/ 5 = 3
+ (X- )² : (1-3)² = 4, continue to do like this and then we
have the sum of this is 10.
+ Apply the formula. The result is: 1.58
SD

3.3.8. Interquartile range
In descriptive statistics, the interquartile
range (IQR), is a measure of statistical dispersion,
being equal to the difference between the upper
and lower quartiles, IQR = Q3 − Q1

Example 1: if the number of values is odd
Example 2: if the number of values is even

3.3.9. Measurement and Descriptive Statistics
- Statistics based on means and standard deviation
are valid for normally distributed or normal data.
- Typically, these data are used in the most powerful
tests called - parametric statistics. However, if the
data are ordered but grossly non–normal, means
and standard deviations may not give meaningful
answers. Then the median and a nonparametric test
would be preferred.

Measurement and descriptive statistics

More Related Content

What's hot (20)

Viewers also liked (6)

Similar to Measurement and descriptive statistics (20)

More from Phạm Phúc Khánh Minh (14)

Recently uploaded (20)

Measurement and descriptive statistics