Statistics

-- B. Kedhar Guhan --
-- X D --
-- 34 --

In this PPT, we would first recap what we had learnt
in 9th.-

• Histograms : SLIDE 3

• Frequency polygons: SLIDE 4

• Numerical representatives of ungrouped data:
SLIDE 5

Then we sneak-a-peek on-

 Central Tendencies of a Grouped Data: SLIDE 7
 Grouped Data : SLIDE 8
 Mean of a grouped data: SLIDE 9
 Direct Method: SLIDE 11
 Assumed mean method: SLIDE 13
 Step deviation Method: SLIDE 15
 Mode: SLIDE 16
 Concept of Cumulative Frequency: SLIDE 17
• Median: SLIDE 18
• Ogives : SLIDE 20

 A Histogram displays a range of values of a
variable that have been broken into groups or
intervals.
 Histograms are useful if you are trying to graph a
large set of quantitative data
 It is easier for us to analyse a data when it is
represented as a histogram, rather than in other
forms.

 Midpoints of the interval of corresponding rectangle
in a histogram are joined together by straight lines. It
gives a polygon
 They serve the same purpose as histograms, but are
especially helpful in comparing two or more sets of
data.

1. Arithmetic Mean: (or Average)
• Sum of all observation divided by
the Number of observation.
• Let x1,x2,x3,x4 ….xn be obs.( thus
there are „n‟ number of scores)
Then Average =
(x1+x2+x3+x4 ….+xn)/n

2 Median: When the data is arranged
in ascending or descending order,
the middle observation is the
MEDIAN of the data. If n is even,
the median is the average of the
n/2nd and (n/2+1/2 )nd observation.

3 Mode: It is the observation that has
the highest frequency.

 A grouped data is one which is
represented in a tabular form with the
observations (x) arranged in
ascendingdescending order and
respective frequencies( f ) given.

 To obtain the mean,
1. First, multiply value of each observation(x) to
its respective frequency( f ).
2. Add up all the obtained values(fx).
3. Divide the obtained sum by the total no. of
observations.

MEAN =

 Lets find the mean of the given data.
Marks 31 33 35 40
obtained (x)

No. of 2 4 2 2
students (f )

Lets find the Σfx and Σf.
x f fx

Xi 31 Fi 2 FiXi 62
Xii 33 Fii 4 FiiXii 144
Xiii 35 Fiii 2 FiiiXiii 70
Xiv 40 Fiv 2 FivXiv 80
Σf = 2+2+2+4 = 10 Σfx = 62+144+70+80 = 356

So, Mean = Σfx = 356 =35.6
Σf 10

 Often, we come across sets of data with class
intervals, like:
Class 10-25 25-40 40-55 55-70 70-85 85-100
Interval
No. os 2 3 7 6 6 6
students

To find the mean of such data , we need
a class mark(mid-point), which would
serve as the representative of the whole
class.
Class Mark = Upper Limit + Lower Limit
2
**This method of finding mean is known as DIRECT METHOD**

 Lets find the class mark of the first class of the given table.
Class Mark = Upper Limit(25) + Lower Limit(10)
2
= 35 = 17.5
2
Similarly, we can all the other Class
Marks and derive this following table:

C.I. No. of students(f ) C.M (x) fx Now,
10-25 2 17.5 35.0
mean = Σfx
25-40 3 32.5 97.5
40-55 7 47.5 332.5
Σf
55-70 6 32.5 375.0 = 1860
70-85 6 77.5 465.0 30
85-100 6 92.5 555.0
Total Σf=30 Σfx=1860.0 = 62

 Another method of finding MEAN:
1. Choose one of the observation as the “Assumed
Mean”. [select that xi which is at the centre of
x1, x2,…, xn.
2. Then subtract a from each class mark x to
obtain the respective d value (x-a).
3. Find the value of FnDn, where n is a particular
class; F is the frequency; and D is the obtained
value.

Mean of the data= mean of
the deviations =

1. Follow the first two steps as in Assumed Mean
method.
2. Calculate u = xi-a
h

3. Now, mean = x = a+h { },
Σ fu
Σf

Where
h=size of the CI
f=frequency of the modal class
a= assumed mean

The class with the highest frequency is
called the MODAL CLASS
C.I. No. of C.M fx
students(f ) (x) In this set of
10-25 2 17.5 35.0 data, the class
25-40 3 32.5 97.5
“40-55” is the
40-55 7 47.5 332.5
55-70 6 32.5 375.0
modal class as
70-85 6 77.5 465.0 it has the
85-100 6 92.5 555.0 highest
Total Σf=30 Σfx=1860
frequency

 It‟s the „running total‟ of frequencies.
 It‟s the frequency obtained by adding the of all
the preceding classes.
 When the class is taken as less than [the Upper
limit of the CI], the cumulative frequencies is
said to be the less than type.
 When the class is taken as more than [the lower
limit of the CI], the cumulative frequencies is
said to be the more than type.

 If n ( no. of classes) is odd, the median is
{(n+1)/2}nd class.
 If n is even, then the median is the average of
n/2nd and (n/2 + 1)th class.
 Median for a grouped data is given by
Median = l{ n/2f- cf }h
Where
l= Lower Limit of the class
n= no. of observations
cf= cumulative frequency of the preceding class
f= frequency
h= class size

 Cumulative frequency distribution can be
graphically represented as a cumulative
frequency curve( Ogive )

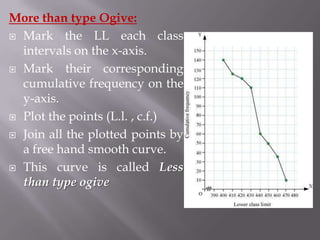
More than type Ogive:
 Mark the LL each class
intervals on the x-axis.
 Mark their corresponding
cumulative frequency on the
y-axis.
 Plot the points (L.l. , c.f.)

 Join all the plotted points by
a free hand smooth curve.
 This curve is called Less
than type ogive

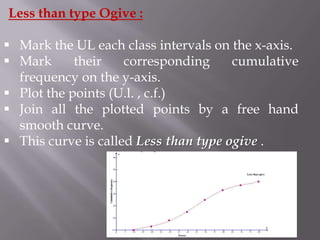
Less than type Ogive :

 Mark the UL each class intervals on the x-axis.
 Mark their corresponding cumulative
frequency on the y-axis.
 Plot the points (U.l. , c.f.)
 Join all the plotted points by a free hand
smooth curve.
 This curve is called Less than type ogive .

METHOD 1
 Locate n/2 on the y-axis.
 From here, draw a line parallel to x-axis, cutting
an ogive ( less/more than type) at a point.
 From this point, drop a perpendicular to x-axis.
 The point of intersection of this perpendicular
and the x-axis determines the median of the
data.

METHOD 2:

 Draw Both the Ogives of the data.
 From the point of intersection of these
Ogives, draw a perpendicular on the x-axis.
 The point of intersection of the
perpendicular and the x-axis determines.

Statistics

More Related Content

What's hot (20)

Viewers also liked (11)

Similar to Statistics (20)

More from Kedhar Guhan (11)

Statistics