Biostatistics

Contents:
• Introduction
• Basic terminology
• Scales of measurement
• Data
• Presentation of data
• Measures of Dispersion
• References

What do STATISTICS mean?
› Statistics or Datum means a
measured or counted fact or piece of
information stated as a figure.
› Statistics is an absolutely
indispensable tool ,providing the
techniques that allow researchers to
draw objective scientific conclusions

Why do we need statistics?
“When you can measure what you are speaking about
and express it in numbers ,you know something about
it. But when you cannot measure and cannot express it
in numbers, your knowledge is of meagre and
unsatisfactory kind”
-LORD KELVIN

Biostatistics
› It is an art and science of collection, compilation, presentation, analysis and logical
interpretation of biological data affected by multiplicity of factors.
› It is the term used when the tools of statistics that emphasizes the statistical
applications in the biomedical and health sciences
› John Graunt-Father of health statistics

› Biostatistics can also be called:-
 Quantitative medicine
 Science of variations
For such studies we need mathematical techniques called as
statistical method

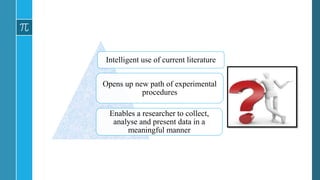
• To read the literature critically, assessing the adequacy
of the research and interpreting the results and conclusions
correctly so that they may properly implement the new
discoveries in diagnosis and treatment – understanding
statistics sufficiently is required.
Intelligent use of current literature
Opens up new path of experimental
procedures
Enables a researcher to collect,
analyse and present data in a
meaningful manner

Basic Terminology
• In most cases, the biomedical and health sciences data consists of observations
of certain characteristics of individual subjects, experimental animals,
chemicals, microbiological, or physical phenomena in laboratories, or
observations of patients, responses to treatment.
• Whenever an experiment or a clinical trial is conducted, measurements are taken
and observations are made.

• Some data are numeric, such as height (5’6”), systolic
B.P. (112mm Hg), and some are non-numeric, such as sex
(female, male) and the patient’s level of pain (no pain,
moderate pain, severe pain).
• To adequately discuss and describe that data, few terms
that will be used repeatedly are defined.

Population
• The collection of all elements of interest having one or more common
characteristics is called a population.
• The elements can be individual subjects, objects, or events.
• The population that contains an infinite number of elements is called an infinite
populations.
• The population that contains an finite number of elements is called an
finite populations.

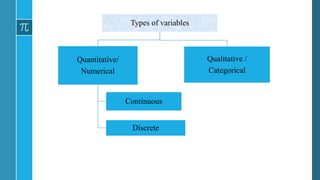
Variable
• A variable is any characteristic of an object that can be measured or categorized.
• Denoted by an upper case of the alphabet, X, Y, or Z.
E.g.
Age
Sex
Waiting time in clinic
Diabetic levels

Types of variables
Quantitative/
Numerical
Discrete
Continuous
Qualitative /
Categorical

Qualitative Variable:
It is a characteristic of people or objects that cannot be naturally expressed
in a numeric value.
E.g.:
Sex – male, female
Facial type – Brachyfacial, Dolichofacial, Mesiofacial
Level of oral hygiene – poor, fair, good

Quantitative Variable:
It is a characteristic of people or objects that can be naturally expressed
in a numeric value.
E.g.
Age
Height
Bond strength

Discrete Variable:
It is a random variable that can take on a finite number of values or a
countable infinite number (as many as there are whole numbers) of values.
E.g.:
• The size of a family
• The number of DMFT teeth. T can be any one of the 33 numbers,
0,1,2,3,…32.

Continuous Variable:
It is a random variable that can take on a range of values on a continuum, i.e.,
its range is uncountably infinite.
E.g.:
Treatment time
Temperature
Torque value on tightening an implant abutment

Confounding Variable:
The statistical results are said to be confounded when the results can have
more than one explanation.
E.g.: In a study, smoking is the most important etiological factor in the
development of oral squamous cell carcinoma. It has been suggested that
alcohol is one of the major causes of squamous cell carcinoma, and alcohol
consumption is also known to be closely related to smoking. Therefore, in this
study, alcohol is confounding variable.

• Introduction ✔
• Basic terminology✔
• Scales of measurement
• Data
• Presentation of data
• References

Nominal Measurement Scale:
It is the simplest type of data, in which the values are in
unordered categories.
E.g.:
• Sex (F, M)
• Blood type (A, B, AB and O)
The categories in a nominal measurement scale have no
quantitative relationship to each other.
Scales Of Measurement:

Ordinal Measurement Scale:
The categories can be ordered or ranked.
The amount of the difference between any two categories, though they
can be ordered, is not quantified.
E.g.:
Pain after separator placement
0 - no pain
1 - mild pain
2 - moderate pain
3 - severe pain
4 - extremely severe pain
Only for statistic convenience

Interval Measurement Scale:
Observations can be ordered, and precise differences between units of
measure exist. However, there is no meaningful absolute zero.
E.g.:
• IQ score representing the level of intelligence.
IQ score 0 is not indicative of no intelligence.
• Statistics knowledge represented by a statistics test score.
The test score zero does not necessarily mean that the
individual has zero knowledge in statistics.

Ratio Measurement Scale:
It is as same as interval scale in every aspect except that measurement
begins at a true or absolute zero.
E.g.:
• Weight in pounds.
• Height in meters.
There cannot be negative measurements.

Observations
• The description of observations:
It includes collecting, summarizing and presenting.
It is also known as Descriptive statistics.
• The inference of observations:
It includes analyzing and interpreting.
It is known as Inferential statistics.

Data
› Whenever an observation is made, it will be recorded and a collective
recording of these observations, either numerical or otherwise is
called DATA

Data
Types of Data
Primary Data
Secondary
data
Qualitative
data
Quantitative
data
Data are a set of values of one or more variables recorded on
one or more individuals.

Primary data:
It is the data obtained directly from an individual.
Advantages
I. Precise information
2. Reliable
Disadvantages
I. Time consuming
Secondary data:
It is obtained from outside sources,
e.g. hospital records, school register.

Quantitative data:
Measure something with a number.
E.g: the amount of crowding, overjet, incisor
inclination, and maxillomandibular skeletal discrepancy.
Qualitative data:
Data is collected on the basis of attribute or qualities.
E.g: The sex of the patient, severity of mandibular plane
angle (high, normal, low), likelihood of compliance with
headgear or elastics (yes/no).

Uses Of Data:
In designing a health care programme.
In evaluating the effectiveness of an
on going program.
In determining the needs of a specific
population. .
In evaluating the scientific accuracy of
a journal article.

Method of collection of
data
Questionnaires Surveys Records Interviews

Need for organising the DATA
› The goal is to summarise and present data in useful ways to
support prompt and effective decisions

Presentation of Data:
Methods of presentation of data
Tabulation Diagrams/graphs

Tabulation
Types of Tables
Simple table Master table
Frequency
distribution table

Guidelines for Tabular Presentation
1. Table must be numbered
2. Title- Brief and self explanatory title should be given
3. The heading of columns and rows must be clear, sufficient, concise and
fully defined
4. The data must be presented according to size of importance
5. Full details of deliberate exclusions in collected series must be given

5. Table should not be too larges
6. Figures needing comparison should be placed as close as possible
7. Arrangement should be vertical
8. Foot notes should be given whenever necessary.

Graphs And Diagrams
Impact on
imagination
Better retained in
memory
Easy
comparisons

Bar Charts
A diagram of columns or bars, the height of the bars determine the value of
the particular data in question.
Simple bar graph
Multiple bar graph
Component bar graph

Pie Charts:
58%
23%
10%
9%
Distribution of Malocclusions in school children
class 1 class 2A class 2B class 3
These are so called because the entire graph looks like a pie
and its components represent slices cut from a pie.

Line Graph:
When the quantity is a continuous variable i.e., time or temperature,
data is plotted as a continuous line.
0
1
2
3
4
5
6
Category 1 Category 2 Category 3 Category 4

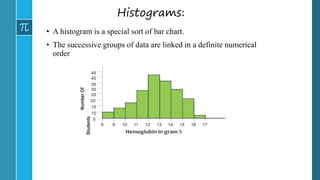
Histograms:
• A histogram is a special sort of bar chart.
• The successive groups of data are linked in a definite numerical
order
Haemoglobin levels of Students in a class

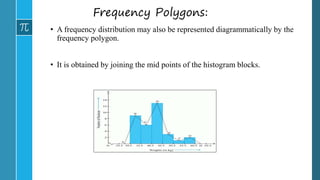
Frequency Polygons:
• A frequency distribution may also be represented diagrammatically by the
frequency polygon.
• It is obtained by joining the mid points of the histogram blocks.

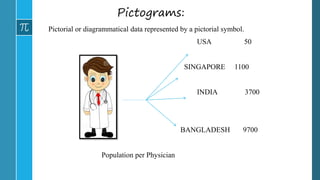
Pictograms:
Pictorial or diagrammatical data represented by a pictorial symbol.
USA 50
SINGAPORE 1100
INDIA 3700
BANGLADESH 9700
Population per Physician

• Scales of measurement ✔
• Data ✔
• Presentation of data ✔
• References

Central Tendency / Statistical Averages:
• Central tendency refers to the center of the distribution of data points.
• Statistics/parameters as the
Mean (the arithmetic average)
Median (the middle datum)
Mode (the most frequent score).
Objectives
•To condense the entire mass of data.
•To facilitate comparison.

Mean
• This measure implies the arithmetic average or arithmetic
mean.
• It is obtained by summing up all the observations and
dividing the total by number of observations.
E.g. The following gives you the fasting blood glucose levels of a sample
of 10 children.
1 2 3 4 5 6 7 8 9 10
56 62 63 65 65 65 65 68 70 71
Total Mean = 650 / 10 = 65
Mean is denoted by the sign X (X bar)

Advantages:
Easy to calculate
Easily understood
Utilizes entire data
Affords good comparison
Disadvantages:
Mean is affected by extreme values, In such cases it leads
to bad interpretation.

Median
• In median the data are arranged in an ascending or descending order of magnitude
and the value of middle observation is located.
Arrange them in ascending or descending order.
71,75,75,77,79,81,83,84,90,95.
Median = 79 + 81 / 2 = 80
If there are only 9 observations then median = 79.
Advantages:
1. It is more representative than mean.
2. It does not depend on every observations.
3. It is not affected by extreme values.

Mode
Mode is that value which occurs with the greatest frequency.
A distribution may have more than one mode.
E.g. Diastolic blood pressure of 10 individuals.
85,75,81,79,71,80,75,78,72,73
Here mode = 75 i.e. the distribution is uni-modal
85,75,81,79,80,71,80,78,75,73
Here mode =75 and 80 i.e. the distribution is bi-modal.

Advantages :
1. It eliminates extreme variation.
2. Easy to understand
Disadvantages :
1. In small number of cases there may be no mode at all because
no values may be repeated; therefore it is not used in medical
or biological statistics.

Dispersion
Dispersion is the degree of spread or variation of the variable about a central
value. The measures of dispersion helps us to study the spread of the values
about the central value.
Purpose of Measures of Dispersion
1. To study the variability of data.
2. To determine the reliability of an average.
3. Compare two or more series in relation to their variability.

Methods of
dispersion
The range Mean deviation
Standard
deviation

The Range:
The range is defined as the difference between the highest
and lowest figures in a given sample.
• It is by far the simplest measure of dispersion.
Advantage:
• Easy to calculate
Disadvantages:
• Unstable
• It is affected by one extremely high or low score.

The Mean Deviation:
• It is the average of deviations from the arithmetic mean.
• It is given by,
M.D. =  (X – Xi)
n

Standard Deviation
• The standard deviation is the most frequently used measure of deviation.
• In simple terms it is defined as Root Mean Square deviation because it is
the square root of the variance (average of the squared difference from the
mean)
• It is denoted by the Greek letter  or by the initials
S.D.  = (X – Xi)2
 n
• Greater the S.D. greater will be the magnitude of
dispersion from mean.
• A small S.D. means a higher degree of uniformity of
observations.

The Normal Curve / Normal
Distribution/ Gaussian Distribution
When a data is collected from a very large number of people and a
frequency distribution is made with narrow class intervals , the
resulting curve is smooth and symmetrical and it is called normal
curve.

Standard Normal Curve
• It is bell shaped .
• The curve is perfectly symmetrical based on an infinitely large number of
observations.
• The total area of curve is one, its mean is zero and standard deviation is
one.
• All the three measures of central tendency , the mean,
median and mode coincide

Probability
• Probability is defined as possible or probable chances of occurrence of an event
or happening. Probability is a proportion.
• In tossing a coin, the only possible outcome is a head or a tail. Probability of a
head is 0.5 and tail is 0.5 and the sum is 1.

If the probability is more than 0.05, the difference is called
insignificant and if it is less than (or) equal to 0.05 the difference is
called as significant. This value of P is obtained by calculating
various tests of significance.
P < 0.001 Very highly significant
P < 0.01 Highly significant
P < 0.05 Significant.
P > 0.05 not Significant.

• Scales of measurement ✔
• Data ✔
• Presentation of data ✔
• Measures of Dispersion ✔
• References

REFERENCES:
•Biostatistics for oral healthcare – Jay S. Kim, Ronald J. Dailey
•Essentials of public health dentistry- Soben Peter
•Park text book of Community Medicine
•Orthodontics: Current principles and techniques. Graber, Vanarsdall,
Vig
59

Biostatistics

More Related Content

What's hot (20)

Similar to Biostatistics (20)

Recently uploaded (20)

Biostatistics

Editor's Notes