Basic Concepts of Statistics - Lecture Notes

Atmiya Institute of Technology & Science – General Department Page 1
B.E. Sem-IV
Sub: NUMERICAL AND STATISTICAL METHODS FOR COMPUTER ENGINEERING
(2140706)
Topic: Basic Concepts of Statistics
 Introduction
The word “Statistics” appears to have been derived from the Latin word Status or the Italian word
Statista, both meaning a “manner of standing” or “position”
Statistical techniques have been widely used in many diverse area of scientific investigation.
The application of statistics is broad indeed and includes business, marketing, economics, agriculture,
education, psychology, sociology, anthropology and biology in addition to our special interest
computer science.
 Some Statistical Terms
Data are obtained largely by two methods
(a) By counting - for example, the number of days on which rain falls in a month for each month
of the year, and
(b) By measurement - for example, the heights of a group of people.
Discrete and continuous data
When data are obtained by counting and only whole numbers are possible, the data are called
discrete. For example:- the number of stamps sold by a post office in equal period of time.
Measured data can have any value within certain limits are called continuous. For example:- the time
that a battery lasts is measured and can have any value between certain limits.
Set, population and sample
A set is a group of data and an individual value within the set is called a member of the set.
For example:- if the weights of five students are measured correct to the nearest 0.1 kg are found to
be 53.1 kg, 59.4 kg, 62.1 kg, 72.8 kg and 64.4 kg, then the set of weights in kilograms for these
students is {53.1, 59.4, 62A, 77.8, 64.4} and one of the member of set is 77.8
A set containing all the numbers is called a population. Some members selected at random from a
population are called a sample.

Basic of Statistics
For example:- Thus all scooter registration numbers form a population, but the registration numbers
of say, 10 scooters taken at random throughout the country are a sample drawn from that
population.
Frequency and relative frequency
The number of times that the value of a member occurs in a set called the frequency of that
member. For example:- In the set : {2, 3, 4, 5, 4, 2, 4, 7, 9}, the member 4 has a frequency of three,
member 2 has a frequency 2 and the other members have a frequency of one.
The relative frequency with which any member of a set occurs is given by the
ratio =
frequency of a member
total frequency of all members
For example:- For the set: {2, 3, 5, 4, 7, 5, 6, 2, 8}, the relative frequency of member 5 is 2/9.
Often, relative frequency is expressed as a percentage and the percentage relative frequency is
(relative frequency X 100)%
E.g:- Data are obtained on the topics given below. State whether they are discrete or continuous.
(a) The amount of petrol produced daily for each of 31 days by a refinery
(b) The number of bottles of milk delivered daily by each of 20 milkmen,
(c) The time taken by each of 12 athletes to run 100 meters.
(d) The number of defective tablets produced in each of 10 one—hour periods by a machine.
Ans:- (a) (b) (c) (d)
 Data analysis
Presentation of Ungrouped Data
When the number of members in a set is small say ten or less, the data can be represented
diagrammatically without further analysis, these include
(a) Pictograms or Picture diagrams
It is a popular method to express the frequency of occurrence of events to a common man
such as attacks, deaths, number operated, accidents in a population. In which pictorial
symbols are used to represent quantities in horizontal line.

Basic of Statistics
E.g.:- The number of television sets repaired in a workshop by a technician in six, one month period is
as shown below. Present these data as a pictogram.
Month Number of TV’s repaired
January 11
February 6
March 15
April 9
May 13
June 8
Ans:-
Month Number of TV sets repaired = 2 sets
January
February
March
April
May
June
Each symbol shown in above table represents two television sets repaired. Thus in January 5 1/2
symbols are used to present the 11 sets repaired, in February 3 symbols are used to represent the 6
sets repaired and so on.
(b) Bar charts or Bar diagrams
Bar chart or diagram is a popular and easy method adopted for visual comparison of the
magnitude of different frequencies in discrete data. . Bars may be drawn in ascending or
descending order of magnitude or in the serial order of events. Spacing between any two bars
should be nearly equal to half of the width of the bar.
The data represented by equally spaced horizontal rectangles is called horizontal bar charts
and the data represented by equally spaced vertical rectangles is called vertical bar charts.

Basic of Statistics
E.g.:- The distance in kilometers travelled by 4 salesman in a week are as shown below.
Salesman P Q R S
Distance travelled (km) 413 264 597 143
Use horizontal bar chart to represent these data diagrammatically.
Ans:-
Distance travelled (km)
E.g.:- The number of issues of tools from a store in a factory is observed for seven, one-hour periods
in a day and the results of the survey are as follows:
Period 1 2 3 4 5 6 7
Number of issues 34 17 9 5 27 13 6
Present these data on vertical bar chart.
Ans.:-
Salesman

Basic of Statistics
(c) Pie diagram:
In a pie diagram, the area of a circle represents the whole and the areas of the sectors of the
circle are made proportional to the parts which make up the whole.
E.g.:- The retail price of a product costing Rs. 2 is made up as follows: materials 10p, labour 20p,
research and development 40p, overheads 70p, profit 60p. Present these data on pie diagram.
Ans.:- A circle of any radius is drawn, and the area of the circle represents the whole, which in this
case is Rs. 2. The circle is subdivided into sectors, so that the areas of the sectors are proportional to
the parts i.e., the parts which make up the total retail price. For the area of a sector to be
proportional to a part, the angle at the centre of the circle must he proportional to that part. The
whole, Rs. 2 or 200p, corresponds to 360
◦
.
Therefore
10p corresponds to
10
360
200
 degrees = ______
◦
20p corresponds to 360
200
 degrees = ______
◦
200
 degrees = ______
◦
200
 degrees = ______
◦
200
 degrees = ______
◦
The pie diagram is shown below:

Basic of Statistics
 Presentation of Group data – Frequency Distributions
Variable
A quantity which can vary from one individual to another is called a variable. It is also called a
variate. For example:- Wages, rain fall records, heights and weights.
Quantities which can take any numerical value within a certain range are called continuous variables.
For example:- The height of a child at various ages is continuous variable since as the child grows
from 120 cm to 150 cm his height assumes all possible values within the limit.
The quantities which are incapable of taking all possible values are called discontinuous or discrete
variable. For example:- The number of rooms in a house can take only the integral values such as 2,
3, 4 etc.
Frequency Distributions
If some values of a variate are collected in arbitrary order in which they occur, the mind cannot
properly grasp the significance of the data.
For example:- The number of miles that the employees of a large department store traveled to work
each day
1 2 6 7 12 13 2 6 9 5
18 7 3 15 15 4 17 1 14 5
4 16 4 5 8 6 5 18 5 2
9 11 12 1 9 2 10 11 4 10
9 18 8 8 4 14 7 3 2 6
The data is given in the crude (or raw) form. The data given in this form is called ungrouped data. If
the data is arranged in ascending or descending order of magnitude it is said to be arranged in an
array.
The range of the data is the value obtained by taking the value of the smallest member from that of
the largest number.
The data shows the range= ______ - _______ = _________

Basic of Statistics
The size of each class is given approximately by range divided by the number of classes.
Suppose 6 classes are required, then the size of each class is
________ / ________ = _________ approximately.
To achieve six equal classes spanning a range of values from 1 to 18, the class-intervals are selected as
1 – 3 , 4 – 6, _____ - _______ ,
This method of arrangement is called a tally method or tally diagram.
Table:1
Class Tally
Class mid-
point
Frequency
Commutative
Frequency

Basic of Statistics
Those members having similar values are grouped together; such groups are called classes and the
boundary ends
_____, ______, _____, ______, _____, ______,
called class limits.
In the class limits 1 – 3 , 1 is the lower limit, 3 is the upper limit. The difference between upper and
lower limits of a class is called its magnitude or class-interval. For example:- class-interval of the class
of the class 1-3 is 2.
The number of observations falling with in a particular class is called its frequency or class frequency.
For example:-The frequency of the class __________ is ________.
The variate value which lies mid-way between the upper and lower limit is called mid-value or mid-
point of that class.
The cumulative frequency corresponding to a class is the total of all the frequencies up to and
including that class.

Basic of Statistics
 Graphical Representation of Grouped Data
Generally the following types of graphs are used in representing frequency distributions:
(1) Histogram
(2) Frequency polygon and frequency curve
(3) Ogive or Cumulative frequency distribution curve
(1) Histogram
One of the principal ways of presenting grouped data diagrammatically is by using a
histogram in which the areas of vertical, adjacent rectangles are made proportional to
frequencies of the classes.
When class intervals are equal, the heights of the rectangles of histograms are equal to the
frequencies of the classes.
For histograms having unequal class intervals, the area must be proportional to the
frequency. For example:- Hence, if the class interval if class A is twice the class interval of class
B, then for equal frequencies, the height of rectangle representing A is half that of B.
E.g.:- Construct a histogram for the data given in Table:1
Class mid-point value
The width of the rectangles corresponding to upper class boundary values minus the lower class
boundary values and the heights of the rectangles correspond to the class frequencies.

Basic of Statistics
(2) Frequency polygon and Frequency curve
Frequency polygon is a graph obtained by plotting frequency against mid points values and
joining the co—ordinates with straight lines.
If the class intervals are very small the frequency polygon assumes the form of a smooth
curve known as the frequency curve.
E.g.:- Draw the frequency polygon for the data given in the table.
Class Class mid-point Frequency
7.1 - 7.3 7.2 3
7.4 – 7.6 7.5 5
7.7 – 7.9 7.8 9
8.0 – 8.2 8.1 14
8.3 – 8.5 8.4 11
8.6 – 8.8 8.7 6
8.9 – 9.1 9.0 2
Class mid-point vlaue
A frequency polygon is shown in Fig, the co—ordinates corresponding to the class mid—point
verses frequency values given in Table.
Frequency

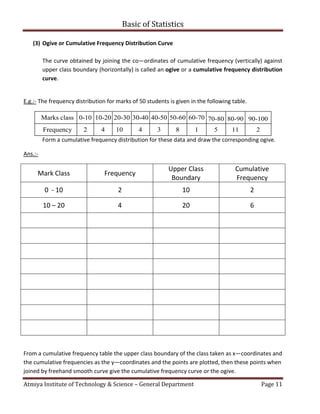
Basic of Statistics
(3) Ogive or Cumulative Frequency Distribution Curve
The curve obtained by joining the co—ordinates of cumulative frequency (vertically) against
upper class boundary (horizontally) is called an ogive or a cumulative frequency distribution
curve.
E.g.:- The frequency distribution for marks of 50 students is given in the following table.
Marks class 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100
Frequency 2 4 10 4 3 8 1 5 11 2
Form a cumulative frequency distribution for these data and draw the corresponding ogive.
Ans.:-
Mark Class Frequency
Upper Class
Boundary
Cumulative
Frequency
0 - 10 2 10 2
10 – 20 4 20 6
From a cumulative frequency table the upper class boundary of the class taken as x—coordinates and
the cumulative frequencies as the y—coordinates and the points are plotted, then these points when
joined by freehand smooth curve give the cumulative frequency curve or the ogive.

Basic of Statistics
Upper Class Boundary
Frequency

Basic Concepts of Statistics - Lecture Notes

More Related Content

What's hot (20)

Similar to Basic Concepts of Statistics - Lecture Notes (20)

More from Dr. Nirav Vyas (20)

Recently uploaded (20)

Basic Concepts of Statistics - Lecture Notes