Statistics for DP Biology IA

STATISTICS FOR THE DP BIOLOGY Feb 2022
V. Garga, MSc

OUTLINE
1. Why statistics is important?
2. Types of data and sample size
3. Analysis of the mean, range and distribution
4. Standard deviation and standard error
5. Significant figures and outliers
6. Types of graphs
7. Linear regression
8. Pearson correlation coefficient
9. Spearman rank correlation index
10. T-test
11. ANOVA
12. Post-HOC analysis
13. Chi-squared analysis
14. Choosing the appropriate statistics for the biology IA
Descriptive Inferential

Statistics
Is used to describe the data.
For example: the range, average and
spread of data.
Is used to extend the conclusions from a
small sample to a wider population or
another sample.
For example: t-test, ANOVA and Chi-
squared.

1. WHY STATISTICS IS IMPORTANT?
•We cannot survey every individual organism in the population, so we take a sample, analyse it and
extrapolate the tendencies to the whole population.
•Or an experiment with 5 repeats, and limited resources (money and time constraints), how do we know
whether the difference we see is significant statistically or not?
•So we need some kind of a minimal sample to work with.
•In biology, if we do not do the analysis of statistical significance (if the student just does average and range)
then we should NOT state anything about the significance of the results. We then should talk only about
TENDENCIES in the data, but specify why statistics were not applied to show significance (for example, not
enough time to collect the minimum required sample size etc)
•Biostatistics is a subfield of applied statistics. It is used in public health, medicine and biology. It includes
common conventions used by all researchers when reporting the data.
•Biostatisticians report data with 95% confidence in the result, with 5% chance of mistake.
https://www.youtube.com/watch?v=1Q6_LRZwZrc

ADVICE FROM IB
•Statistical analysis is expected.
•Percentages, means, standard deviations or other statistics at the end of the column or
row of data they represent will be sufficient.
•For more complex processing using spreadsheets, screenshots are acceptable.
•For other less orthodox processing, a worked example may be necessary.
•The questions that the teacher should be asking are:
• Is the processing appropriate?
• Can the processing be followed?
• Is the processing correct?
• Are conclusions in line with the degree of the data processing?
IB, May 2021

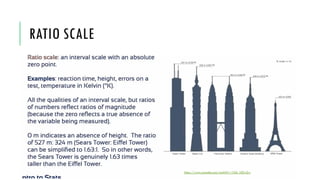
2. TYPES OF DATA AND SAMPLE SIZE
•The more data the stronger is the conclusion
•We are limited to 10 hours of data collection and analysis
•We are also limited by a school budget and available materials
•Sample size should be also reflecting the uncertainty and variability of the measurements, the
larger the uncertainty the bigger should be the sample. For example measurements in humans,
measurements in length of the seedlings etc.
•Biochemical reactions (titration, enzyme activity) can be set up with more controlled variables
and measured with less variabity.
•n – sample size
•Sample size should be large enough to represent the population. For example in quadrant
studies the sample size would be 10% of the total area. In school lab environment this is
constrained by time and resources

https://w55e0y989ilejyz-s-a2157.bj.tsgdht.cn/watch?v=1Q6_LRZwZrc

When collecting data we make measurements

NOMINAL

ORDINAL

INTERVAL SCALE

RATIO SCALE

https://w55e0y989ilejyz-s-a2157.bj.tsgdht.cn/watch?v=1Q6_LRZwZrc 28 min

SAMPLE SIZE
• Sample size depends on the type of data and can be designed with the statistical approach in mind.
• Students will have 10 hours to collect data. So online investigations will require a much larger sample size
than physical investigations.
• If less than a minimum (5) measurements are taken then results will be inconclusive, but still can be
described and evaluated.
• In order to do standard deviation, we need at least 5 measurements.
• 5-14 measurements, therefore, is a minimum for biology IA experiments and is called a very small sample
size.
• 15-30 is a small sample.
• >30 is considered a large sample
• Students need to discuss the limitations of their sample size.
IB, May 2020

3. ANALYSIS OF THE MEAN, RANGE AND
DISTRIBUTION
•In biological data mean and average are the same thing. Be
careful that the student in the report uses one or the other.
•The range shows the extent from minimum to maximum values.
The larger the range the more the data spread around the
mean.
•The distribution shows us how often each value occurs in the
data set.
Sample data set: 3 5 4 7 2 3 9
n: 7
X: 4.71 ≈ 5
Range: 7
Crashcourse statistics #3
https://www.youtube.com/watch?v=kn83BA7cRNM&list=PL8dPuuaLjXtNM_Y-bUAhblSAdWRnmBUcr&index=4
https://cdn.virtualnerd.com/thumbnails/Alg1_14_02_0014-diagram_thumb-lg.png

The mean is always distorted by outliers. Therefore it is
important for students to discuss this in their report.
During this discussion, students may indicate what is the
mode of the data.
Mode is the value which appears the most in the set.
There could be more than one mode.
Mode is only useful though if we have a relatively
large sample. Smaller samples will have no mode.
Sample data set: 3 5 4 7 2 3 9
n: 7
X: 4.71 ≈ 5
Range: 7
Mode: 3
http://www.learnersplanet.com/sites/default/files/images/mean-mode-median.png

Crashcourse statistics #3
https://www.youtube.com/watch?v=kn83BA7cRNM&list=PL8dPuuaLjXtNM_Y-bUAhblSAdWRnmBUcr&index=4

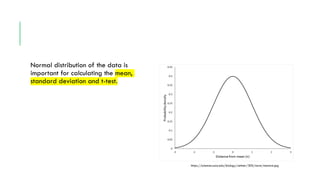
Normal distribution of the data is
important for calculating the mean,
standard deviation and t-test.
https://sciences.usca.edu/biology/zelmer/305/norm/stanorm.jpg

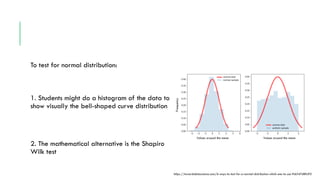
To test for normal distribution:
1. Students might do a histogram of the data to
show visually the bell-shaped curve distribution
2. The mathematical alternative is the Shapiro
Wilk test
https://towardsdatascience.com/6-ways-to-test-for-a-normal-distribution-which-one-to-use-9dcf47d8fa93
Values around the mean Values around the mean
Frequency

SHAPIRO WILK TEST
Shapiro Wilk test
If the p- value of the Shapiro-Wilk Test is larger
than 0.05, we assume a normal distribution.
If the p- value of the Shapiro-Wilk Test is smaller
than 0.05, we do not assume a normal distribution.
H0: Data is normally distributed.
H1: Data is NOT normally distributed.
https://towardsdatascience.com/6-ways-to-test-for-a-normal-distribution-which-one-to-use-9dcf47d8fa93
Online calculator:
https://scistatcalc.blogspot.com/2013/10/shapiro-wilk-
test-calculator.html
Reporting results
Figure 1. Screenshot of the input data Figure 2. Screenshot of the analysis results
According to Shapiro Wilk test of normality, W=0.981889, p>0.05, therefore the
experimental data set is normally distributed.

4. STANDARD DEVIATION AND STANDARD ERROR
•Standard deviation (SD) or standard error of the mean (SEM) can be useful assuming there
is a sufficient number of replicates to be able to calculate one, otherwise, range bars are
acceptable for max-min values.
•SEM requires usually a larger sample size.
•SD can be done on a sample as small as 5.
•SD describes the characteristics of the data set you collected.
•SEM describes how far is your collected sample mean from the larger population mean.
Basically, it talks about how well your data may represent the population.
•Thus, students explain the appropriate meaning of the value based on what they used SD
or SEM.
https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/what-is-the-standard-error-of-a-sample/

SD
https://assets.ltkcontent.com/images/83660/calculating-standard-deviation_0066f46bde.jpg
https://cdn.scribbr.com/wp-content/uploads/2020/09/standard-deviation-in-normal-distributions.png
• SD shows how far from the mean most of the data is.
• It is conventional to report +/-1 SD as the error bars around the mean on the graphs.
• 68% of all data observed under a normal distribution will fall within one standard deviation of the mean. Similarly,
95% falls within two standard deviations, and 99.7% within three.
Penn State. "STAT 500 Applied Statistics: The Empirical Rule." https://online.stat.psu.edu/stat500/lesson/3/3.3/3.3.4 Accessed Jan. 17, 2022

SEM
The larger your sample the smaller will be its
difference from the representative population,
and therefore smaller the SE value.
The SEM takes the SD and divides it by the
square root of the sample size.
https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/what-is-the-standard-error-of-a-sample/
https://www.investopedia.com/ask/answers/042415/what-difference-between-standard-error-means-and-standard-deviation.asp
Altman, Douglas G, and J Martin Bland. “Standard deviations and standard errors.” BMJ (Clinical research ed.) vol.
331,7521 (2005): 903. doi:10.1136/bmj.331.7521.903. Accessed Jan. 17, 2022.
https://www.scribbr.com/statistics/standard-error/

5. SIGNIFICANT FIGURES AND OUTLIERS
•Decimal places in the recorded data should be consistent with degrees of precision.
•Decimal places in the Mean should be the same as in the raw data.
•Uncertainties should appear in the column headings along with the units.
•Uncertainties for counts (±1) are not necessary.
However, data derived from these counts may possess a degree of precision (e.g. percentage
germination of a sample of 25 seeds will have an error margin of ±4% or a heart rate after a 15 s palpation ±4
beats per min). Error propagation is not needed, but it is good if a student shows awareness of this in the
evaluation.
•For other calculated values, two numbers after the decimal point are acceptable when
reporting in high-school sciences.

OUTLIERS
IB, May 2021
• Outliers should not be excluded from processing just because
they do not “fit well” in the general trend of the data.
• Outliers can be identified mathematically.
• Exclusion requires a justification.
• Outliers can only be excluded if there is evidence of a mistake
in the data collection.
• If data was accurately collected, then an outlier actually can
be new insight into the new trend or discovery.
• Outliers’ significance should be discussed taking this into
account.
Example:
Measuring heights in 13 year old boys.
One of the boys is clearly much taller
than others.
Is he an outlier? Mathematically yes, but
it is not a mistake and therefore should
not be excluded. Instead report should
address the possibility of results
affected by age of onset of puberty
and what it means for their choice of
dependent and independent variables.

CALCULATING OUTLIERS
• If a number is less than Q1 – 1.5×IQR or
greater than Q3 + 1.5×IQR, then it is an
outlier.
• Q is the quartile boundary
• The interquartile range (IQR) is a measure of
statistical dispersion, being equal to the
difference between the third quartile (Q3)
and first quartile (Q1), that is, IQR = Q3 –
Q1.
• Students also may use the online calculator:
https://miniwebtool.com/outlier-calculator/
In this case, it should be appropriately
referenced.
https://www.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/box-whisker-plots/a/identifying-outliers-iqr-rule
5, 7, 10, 15, 19, 21, 21, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 24, 25
Example:
Q1 = 19
Q3 = 24
IQR = 24-19 = 5
Q1 - 1.5*IQR = 19-1.5*5 = 11.5 Outliers are 5, 7 and 10.
Q3+ 1.5*IQR = 24+1.5*5 = 31.5 There are no upper
outliers.

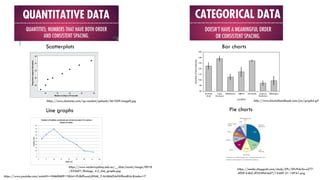
6. TYPES OF GRAPHS
•Graphing is a type of descriptive statistics which helps us to easily make conclusions
about the data. It represents data in a simplified visually engaging format.
•In high school biology, an experimental report graph should serve a purpose.
•Only graphs that are discussed in the report should be included.
•For example ---- graph showing the trend in data over time.
•One graph is enough for the IA.
•By looking at a graph alone reader should easily see the conclusion from the data in
response to the research question asked.

Bar charts
Scatterplots
Line graphs
https://www.youtube.com/watch?v=HMkllhBI91Y&list=PL8dPuuaLjXtNM_Y-bUAhblSAdWRnmBUcr&index=7
Pie charts
http://www.biostathandbook.com/pix/graph4.gif
https://media.cheggcdn.com/study/59c/59c9da3a-e277-
49b9-b4b5-df3549ef4af7/13469-21-1IEFA1.png
https://www.dummies.com/wp-content/uploads/361059.image0.jpg
https://www.westernsydney.edu.au/__data/assets/image/0018
/533601/Biology_4.2_line_graphs.jpg

•A bar chart represents two or more categories
and measurements within those categories.
•Technically it is categorical (IV) and quantitative
(DV) data combined in one chart.
•Therefore, this type of chart is suitable for testing
different conditions or locations, where the
question is which condition/location is the best.
Bar charts
Pie charts
http://www.biostathandbook.com/pix/graph4.gif
https://media.cheggcdn.com/study/59c/59c9da3a-e277-49b9-b4b5-
df3549ef4af7/13469-21-1IEFA1.png
•The pie chart is used only when one category is
applied.
•In Biology IA we insist on 2-5 categories, therefore
this type of chart is not recommended.
•Also, there is no way to express error bars on this
type of chart.

Scatterplots
Line graphs
http://www.saburchill.com/IBbiology/graphs/images/039.jpg
https://www.westernsydney.edu.au/__data/assets/image/0018
/533601/Biology_4.2_line_graphs.jpg
•Scatterplots are the most versatile graph to present
in biology reports.
•Usually, it presents all individual data points against
two measurements.
•Because of this, this is the best graph to represent in
database analyses and in any correlation studies.
•It is possible to just present the averages and SD
from the single condition on the x-axis.
•The line graph is used to show changes over one
continuous range, for example, over time.
•They can be useful for displaying data where other
than a linear relationship is expected between two
variables.
•Most often point represent the averages and SD from
the single condition on the x-axis.
•Line graphs are acceptable in DP biology, but not in
physics or chemistry.

MAKING CUSTOM ERROR BARS ON GRAPHS IN EXCEL
•Note: many students just choose SD suggested by Excel for error
bars. That is incorrect; because Excel will calculate SD between
averages presented in the graph for that option.
•Instead, choose “More error bars options…” and enter the custom
values.
•See the video for reference on how to make error bars:
https://www.youtube.com/watch?v=JeqCl_aD_8Y

REPORTING GRAPHS
•Graphs can be made using Excel or any other program.
•Each graph should have a title.
Example: Graph 1. Mean heights of the seedlings after 8 days of exposure to various salt
concentrations. Error bars represent the SD.
•Error bars, if used on the graphs, should be identified in the title of the graph
(range/SEM/SD).
•Both, y and x axes need to be labelled, with units and uncertainty indicated.
•x is the IV, y is DV.
•The graph should be referenced in the text of the report and appear as close to the
paragraph mentioning it as possible.

OUTLINE
1. Why statistics is important?
2. Types of data and sample size
3. Analysis of the mean, range and distribution
4. Standard deviation and standard error
5. Significant figures and outliers
6. Types of graphs
7. Linear regression
8. Pearson correlation index
9. Spearman rank correlation index
10. T-test
11. ANOVA
12. Post-HOC analysis
13. Chi-squared analysis
14. Choosing the appropriate statistics for the biology IA

7. LINEAR REGRESSION
•Used to predict the values when the line of
best fit is extended. For example – osmolarity
experiments.
• Regression analysis is appropriate
when finding the effect of an “x” variate (IV)
on a “y” variate (DV).
•Regression is used on scatterplot data.
•Regression analysis DOES NOT include
statistics.
http://www.biosci.global/customer-stories-en/pearson-correlation-vs-simple-linear-regression/
Pearson

REPORTING
•Regression analysis will be reported as an equation that fits the data in the scatterplot.
•We can use the resulting equation (there is an option to calculate equation in the Excel) to estimate the
unknown values.
Petal Length = (Petal Width * 1.8693) + 1.7813
https://www.colby.edu/bio/statistics-and-scientific-writing/regression-analysis/

R SQUARED
R2 – describes how well the data fits the trend, on a 0-100% scale.
It can be applied when calculating regression or correlation.
•0% represents a model that does not explain any of the variations in the response variable around its
mean. The mean of the dependent variable predicts the dependent variable as well as the regression
model.
•100% represents a model that explains all the variations in the response variable around its mean.
•R2 calculation is usually done by online calculator or Excel
https://statisticsbyjim.com/regression/how-high-r-squared/
https://www.theseattledataguy.com/wp-content/uploads/2017/09/squared-error-r2.png

8. PEARSON CORRELATION COEFFICIENT
•Important to note that ANY correlation, even if
statistically significant does NOT mean causation.
Students have to be very careful when writing about
this.
•The Pearson coefficient is a measure of the strength
of the linear association
•In order for this test to be valid, all data needs to be
quantitative
https://statistics.laerd.com/statistical-guides/pearson-correlation-coefficient-statistical-guide.php
Requirements for Pearson's correlation coefficient
• Scale of measurement should be interval or ratio
• Variables should be approximately normally distributed
• The association should be linear
• There should be no outliers in the data

R CALCULATIONS
http://faculty.washington.edu/ddbrewer/s231/s231regr.htm
r – is abbreviation for the correlation coefficient
-1 to +1 scale shows the nature of relationship
and strength
https://www.gstatic.com/education/formulas2/397133473/en/correlation_coefficient_formula.svg

REPORTING
• Students do not need to know how to calculate the Person
correlation. They can simply use the online calculator.
• For example
https://www.socscistatistics.com/tests/pearson/default2.
aspx
• When reporting results, the test should be properly
referenced and screenshots of the input and output data
can be included.
• Reporting of the results should always be accompanied
by the graph made by the student (scatter plot with a
line of best fit).
Reporting results
Figure 1. Screenshot of the input
data
Figure 2. Screenshot of the analysis results

REPORTING SIGNIFICANCE
•It is possible to calculate the p-value for Pearson correlation r.
•In this case, N is the number of pairs in your sample. (3 is minimum.)
•Significance level a is a confidence (significance) level in the results
reported.
•Biostatisticians report data with 95% confidence in the result, with a
5% chance of mistake.
•It is accepted as a standard in science reporting that the possibility
of error should not exceed 5%, thus a is always set up to be 0.05.
•At a = 0.05, p values less than 0.05 a reference value will be
deemed significant and p-value more than 0.05 a reference value
will be deemed insignificant.
•The p-value is the probability that you would have found the current
result if the correlation coefficient were in fact zero.
https://statisticsbyjim.com/glossary/significance-level/
https://www.medcalc.org/manual/correlation.php
https://www.webassign.net/bbunderstat9/10-table-06.gif
•If p is lower than the conventional 5%
(p<0.05) the correlation coefficient is
called statistically significant.
•Since p value here is just taking into
account r and N, then you can see that
weaker is the r the more samples are
required for the result to be deemed
significant

REPORTING SIGNIFICANCE
Reporting results
Figure 3. Screenshot of the p calculation.
https://www.socscistatistics.com/tests/pearson/default2.aspx
https://www.webassign.net/bbunderstat9/10-table-06.gif
In the example here the p > 0.05. Therefore indicating that
the results is not statistically significant. So we cannot make
any conclusions applied to the wider population based on
the data analyzed.
Note: students can just report the data as shown in Fig 1-3.
The table of significance above is shown here just for
facilitating our understanding of the values.
p=0.058
a>0.05 a<0.01
n= number of samples

9. SPEARMAN RANK CORRELATION
•Spearman rank correlation is the nonparametric version
of the Pearson correlation.
•Requirements
Scale of measurement must be ordinal for at least one parameter
Data must be in the form of matched pairs
The association must be monotonic (i.e., variables increase in value together, or
one increases while the other decreases)
It can be used when requirements for Pearson test are not met.
https://www.gstatic.com/education/formulas2/397133473/en/spearman_s_ra
nk_correlation_coefficient.svg
https://statistics.laerd.com/statistical-guides/spearmans-rank-order-correlation-statistical-guide.php

REPORTING
• Students do not need to know how to calculate the
Spearman correlation. They can simply use the online
calculator.
• For example
https://www.socscistatistics.com/tests/spearman/default
3.aspx
• When reporting results, the test should be properly
referenced and screenshots of the input and output data
can be included.
• Reporting of the results should always be accompanied
by the graph made by the student (scatter plot with a
line of best fit).
Reporting results
Figure 1. Screenshot of the input
data
Significance table for your reference
n= number of samples

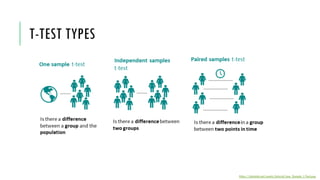
10. T-TEST
•If you want to compare differences in both directions (positive and negative) then it is a two-tailed test.
•For DP biology reports almost always students should use a two-tailed test.
• A one-tailed test is only justified if you have a specific prediction about the direction of the difference (e.g., Group
A scoring higher than Group B), and you are completely uninterested in the possibility that the opposite outcome
could be true.
https://www.statisticssolutions.com/should-you-use-a-one-tailed-test-or-a-two-tailed-test-for-your-data-analysis/
https://keydifferences.com/wp-content/uploads/2017/01/one-tailed-vs-two-tailed-test.jpg
•t-test (Student’s t-test) is used when comparing one or
two sets of data.
• When choosing the t-test you will need to know if your
data is one-tailed or two-tailed.
• If you want to compare overlap in only one direction
then it is a one-tailed test.

T-TEST TYPES
https://datatab.net/assets/tutorial/one_Sample_t-Test.png

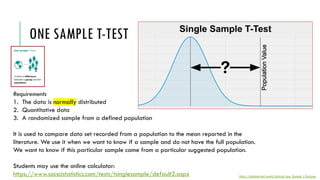
ONE SAMPLE T-TEST
https://datatab.net/assets/tutorial/one_Sample_t-Test.png
Requirements
1. The data is normally distributed
2. Quantitative data
3. A randomized sample from a defined population
It is used to compare data set recorded from a population to the mean reported in the
literature. We use it when we want to know if a sample and do not have the full population.
We want to know if this particular sample came from a particular suggested population.
Students may use the online calculator:
https://www.socscistatistics.com/tests/tsinglesample/default2.aspx

ONE SAMPLE T-TEST- REPORTING
The result (p<0.05) means that the
data set is statistically significantly
different from the expected value.
H0: Sample mean = Hypothesized
Population mean (µ)
H1: Sample mean (x̅) ≠
Hypothesized Population mean (µ)
Reporting results
Figure 1. Screenshot of the input data
https://www.socscistatistics.com/tests/tsinglesample/default2.aspx
https://www.machinelearningplus.com/wp-content/uploads/2020/10/t-table-one-sample-t-test-min.png
df = n - 1

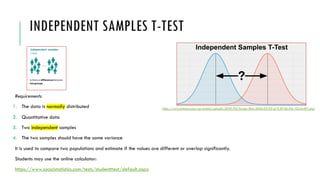
INDEPENDENT SAMPLES T-TEST
Requirements
3. Two independent samples
4. The two samples should have the same variance
It is used to compare two populations and estimate if the values are different or overlap significantly.
https://www.socscistatistics.com/tests/studentttest/default.aspx
https://www.statstest.com/wp-content/uploads/2020/02/Screen-Shot-2020-02-03-at-9.39.36-PM-1024x497.png

INDEPENDENT SAMPLES T-TEST - REPORTING
The result (p>0.05) means that two
data sets are not statistically
significantly different from each
other.
H0: Sample mean of population 1 =
Sample mean of population 2
H1: Sample mean of population 1 ≠
Sample mean of population 2
Reporting results
https://www.socscistatistics.com/tests/studentttest/default2.aspx
https://www.machinelearningplus.com/wp-content/uploads/2020/10/t-table-one-sample-t-test-min.png
The t-value is -1.84173. The p-value is
.090354. The result is not significant at p <
.05.
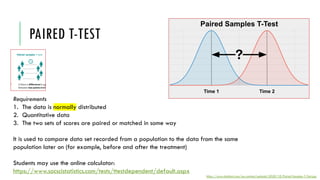
DF=N1 + N2 – 2

PAIRED T-TEST
https://www.statstest.com/wp-content/uploads/2020/10/Paired-Samples-T-Test.jpg
Requirements
3. The two sets of scores are paired or matched in some way
It is used to compare data set recorded from a population to the data from the same
population later on (for example, before and after the treatment)
https://www.socscistatistics.com/tests/ttestdependent/default.aspx

PAIRED T-TEST- REPORTING
The result (p<0.05) means that two
data sets are statistically significantly
different from each other.
H0: Sample mean of population
before = Sample mean of population
after
H1: Sample mean of population
before ≠ Sample mean of population
after
Reporting results
https://www.socscistatistics.com/tests/ttestdependent/default2.aspx
https://cdn1.byjus.com/wp-content/uploads/2019/11/paired-t-test-table.png
The value of t is 6.714549. The value
of p is .00053. The result is significant
at p < .05.
df = n - 1

11. ANOVA
•Data sets should be independent of each other, meaning not the repeat measurements of the
same population (that would be repeated measurement ANOVA).
•There could be one way or two way ANOVA. One way ANOVA is used when only one factor
was measure from all groups; two way ANOVA is used when two factors were measured in all
groups.
•For high school biology most often used is one way ANOVA for independent measurements.
https://www.tibco.com/sites/tibco/files/media_entity/2020-09/anova-diagram.svg
•ANOVA compares the sets of three or
more data simultaneously.
•It is done because repeated t-tests would
give too much cumulative error.

ONE WAY ANOVA REQUIREMENTS
1. The data should be normally distributed.
2. Samples must be independent.
3. Groups must have equal sample size.
• A one-way ANOVA will tell you that at least two groups were different from each other.
But it won’t tell you which groups were different.
• Students will always have to run post-hoc analysis to say exactly which group is
significantly different from others.
• Students don’t need to know how to perform the test, they can just use the online
calculator.
https://www.socscistatistics.com/tests/anova/default2.aspx
https://www.statisticshowto.com/probability-and-statistics/hypothesis-testing/anova/

ANOVA- REPORTING
The result (p<0.05) means that some of
the data sets are statistically significantly
different from others.
H0: there is no difference in sample
means
H1: there is a difference in sample
means
Reporting results
Figure 1. Screenshot of the input data. Treatment 1 is vermicast, treatment 2 is garden
soil , treatment 3 is compost, treatment 4 is sand, treatment 5 is hydroponics medium.
The f-ratio value is 17.01845. The p-
value is < .00001. The result is
significant at p < .05.
Numerator degrees of freedom =
treatments – 1 = t – 1
Denominator degrees of freedom = total
observations minus treatments = N – t
Because there are so many variables in the
ANOVA test, instead of single table there are
separate tables calculated for each level of
significance (a).
https://www.dummies.com/article/business-careers-
money/business/accounting/calculation-analysis/how-to-find-the-critical-values-for-
an-anova-hypothesis-using-the-f-table-146050

12. POST-HOC ANALYSIS
•Post hoc (Latin, meaning “after this”) means to analyze the results of your experimental data
after some previous analysis already conducted.
•The only situation when students are expected to do this in high school biology is a statistically
significant ANOVA result.
•Students don’t need to know how to perform the test, they can just use the online calculator.
•There are many post-hoc tests, but for ANOVA Tukey HSD is recommended.
•Tukey's HSD (honestly significant difference) procedure facilitates pairwise comparisons within
ANOVA data.
https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/post-hoc/

REPORTING POST-HOC RESULTS
Each significant paired Q result (p<0.05) means
that the two sets are statistically significantly
different from one another.
Post hoc comparisons using the Tukey HSD test
indicated that the mean score for the sand condition
(M4 = 6.14) was significantly different from all
other conditions. Also, compost (M3 = 35.57) was
significantly different from hydroponic medium
(M5 = 64.14). However, the compost was not
different from garden soil (M2 = 54.14), or
vermicast (M1 = 57.14). The hydroponic medium
was not different from garden soil, or vermicast.
Students should remember to discuss this result in the
context of their hypothesis. Was the best/worst
result significantly different from others? What are
the trends? Are they as expected?
Reporting results
Figure 3. Screenshot of the post-hoc results of the
same data as in ANOVA example. Treatment 1 is
vermicast, treatment 2 is garden soil , treatment 3 is
compost, treatment 4 is sand, treatment 5 is
hydroponics medium. Significant p values are in blue
ink.
k= Number of Treatments.
Df = SE
For a = 0.05
https://www.real-statistics.com/statistics-tables/studentized-range-q-table/ http://statistics-help-for-
students.com/How_do_I_report_a_1_way_between_subjects_ANOVA_in_APA_
style.htm#.YhC7oBNBzTI

13. CHI-SQUARED ANALYSIS
•The chi-squared test is used to determine whether there is a statistically significant
difference between the expected frequencies and the observed frequencies.
• There are two tests students are expected to know:
Chi-square goodness of fit test
Chi-square test of independence
The chi-squared test is used when one of the parameters is categorical
data.

CHI-SQUARE GOODNESS OF FIT TEST
•The Chi-square goodness of fit test compares experimental data to the expected values.
Example of a question: does the distribution of phenotypes after two hybrid
cross matches the expected outcome?
•While students do learn how to calculate this test by hand in DP Biology syllabus, in the IA and
EE it is not expected for them to do so. They are encouraged to use the online calculator.
https://www.socscistatistics.com/tests/goodnessoffit/default2.aspx
•Note that expected values should be calculated by students based on the observed amount of
data points and then expressed as expected frequencies or ratios.
•Expected value calculations should be reported in the IA and EE.

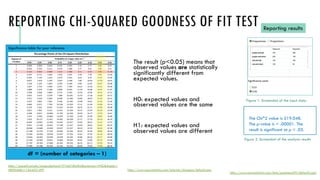
REPORTING CHI-SQUARED GOODNESS OF FIT TEST
The result (p<0.05) means that
observed values are statistically
significantly different from
expected values.
H0: expected values and
observed values are the same
H1: expected values and
observed values are different
Reporting results
Figure 1. Screenshot of the input data.
https://www.socscistatistics.com/tests/goodnessoffit/default2.aspx
The Chi^2 value is 519.048.
The p-value is < .00001. The
result is significant at p < .05.
Numerator degrees of freedom =
treatments – 1 = t – 1
Denominator degrees of freedom = total
observations minus treatments = N – t
https://passel2.unl.edu/image.php?uuid=f744d18faf02&extension=PNG&display=
MEDIUM&v=1644531499 https://www.socscistatistics.com/tutorials/chisquare/default.aspx
df = (number of categories – 1)

CHI-SQUARE TEST OF INDEPENDENCE
The Chi-square test for independence looks for an association between two categorical variables.
Requirements
Random sample
Observations must be independent of each other (so, for example, no matched pairs)
•While students do learn how to calculate this test by hand in DP Biology syllabus, in the IA and EE it is not
expected for them to do so. They are encouraged to use the online calculator.
https://www.socscistatistics.com/tests/chisquare/default2.aspx
•Note that expected values should be calculated by students based on the observed amount of data points and
then expressed as expected frequencies or ratios.
•We expect here that the distribution of data in different data table cells is equal (note – data is adjusted for
the total sample, see the formula below)
•Expected value calculations should be reported in the IA and EE.
Row total * Column total / Sample Size = Expected value for one table cell
Learn more at: https://www.youtube.com/watch?v=7_cs1YlZoug

REPORTING CHI-SQUARED TEST OF INDEPENDENCE
The result (p<0.05) means that the number
of smokers does differ based on the gender.
Further details of the conclusion can be
inferred from the data itself. While the Chi-
squared just tells us if there is association or
not, but does not tell us what it is exactly.
H0: there is no association between two
variables
H1: there is association between two
variables
Reporting results
Figure 1. Screenshot of the input data.
https://www.socscistatistics.com/tests/chisquare/default2.aspx
The chi-square statistic is 5.3333.
The p-value is .020921. Significant
at p < .05.
https://www.statisticssolutions.com/free-resources/directory-of-statistical-
analyses/chi-
square/#:~:text=The%20degrees%20of%20freedom%20for,null%20hypothesis
%20can%20be%20rejected.
https://www.socscistatistics.com/tutorials/chisquare/default.aspx
df = (r-1)(c-1)

SUMMARY OF DIFFERENT STATISTICAL TESTS
Test Used for Type of data Null hypothesis
(unbiased
expectation)
Get CV from a
(significance) of 0.05
Conclusion if p<0.05 Conclusion if p>0.05
(Null hypothesis is true)
T-test Significance of
differences
between two
groups
Two groups
(populations) with
the same variable
measured
Two populations are
the same
DF=n1+n2-1 There is significant difference
between two populations
There is no significant difference
between two populations
Chi-
squared
Differences of
data from
expectations
Two or more
categories
Frequencies
No difference
between expected
and observed data
DF= number of categories
-1
There is a difference between
observed and expected data
There is no difference between
observed and expected data
Pearson Correlation
between two
variables
Group of data
points measured
against two
variables
Two measurements
are not correlated
between each other
DF is number of sample
data pairs
Significant correlation No significant correlation
ANOVA Significance of
differences
between three or
more groups
Several groups
(populations) with
the same variable
measured
No significant
overlap between the
populations
DF= number of groups -1 There are differences between the
groups
There is no difference between the
groups
Tukey post-
HOC
Identifying
groups
significantly
different from
others
Done after
ANOVA
All means are equal

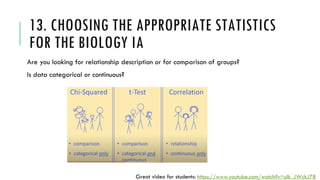
13. CHOOSING THE APPROPRIATE STATISTICS
FOR THE BIOLOGY IA
Are you looking for relationship description or for comparison of groups?
Is data categorical or continuous?
Great video for students: https://www.youtube.com/watch?v=ulk_JWckJ78

Students could use the online questionnaire to determine which test to use, but they
need to know description of their data first.
https://www.socscistatistics.com/tests/what_stats_test_wizard.aspx
Alternative
For not normal distribution
For normal distribution

THANK YOU FOR ATTENTION J
Any questions?
Leave me a message through the website (especially if you notice some mistakes):

Statistics for DP Biology IA

Recommended

More Related Content

What's hot (20)

Similar to Statistics for DP Biology IA (20)

Recently uploaded (20)

Statistics for DP Biology IA