STATISTICS: Hypothesis Testing

HYPOTHESIS TESTING

Prepared by
Roderico Y. Dumaug, Jr.
For Intro to Statistics

Objectives
1) Able to formulate statistical hypothesis
2) Discuss the two types of errors in hypothesis
testing
3) Establish a decision rule for accepting or
rejecting a statistical hypothesis at a specified
level of significance
4) Distinguish between the one-sample case and
two-sample case tests of hypothesis concerning
means
5) Choose the appropriate test statistics for a
particular set of data.

Symbols Applicable
1) Ho – Null Hypothesis
2) H1 – Alternative Hypothesis
3) β – Greek Letter Beta which is the probability of committing a Type 2
Error
4) α – Greek letter Alpha which denotes a probability of committing a
Type 1 Error and is known as the Level of Significance
5) z
6) σ – Greek letter Sigma which means the Variance
7) σx - the standard deviation of the sampling distribution of the mean
8) µ - Greek letter ‘mu’ which is the mean of the normal population
9) n – Sample size
10) - Sample mean
11) t – t distribution; a case where the population standard deviation is
unknown
12) s – standard deviation

Hypothesis Testing: Introduction
• Theory of Statistical Inference: Consists of
methods which one makes inferences or
generalizations about a population. Example is
the Tests of Hypothesis.
• Population vs. Random Sample

Statistical Hypothesis
• Definition: A statistical hypothesis is an assertion or
conjecture concerning one or more populations.
An assumption or statement, which may or
may not be true concerning one or more population.

• Two types of Statistical Hypothesis:
a) The NULL HYPOTHESIS, Ho
b) The ALTERNATIVE HYPOTHESIS, H1
a) Nondirectional Hypothesis– Asserts that one value is different
from another (or others). Also called as the 2-sided Hypothesis.
“Not equal to” or ≠.
a) Directional Hypothesis – An assertion that one measure is Less
than (or greater than) another measure of similar nature. Also
called the 1-sided Hypothesis. “<“ or “>”

Examples of Statistical Hypothesis
1) Ho: The average annual income of all the families in the City is
Php36,000 (µ = Php 36,000).
H1 : The average annual income of all the families in the City is not
Php36,000 (µ ≠ Php36,000).
2) Ho: There is no significant difference between the average life of brand A
light bulbs and that of brand B light bulbs (µA = µB).
H1 : There is a significant difference between the average life of brand A
light bulbs and that of brand B light bulbs (µA ≠ µB).
3) Ho: The proportion of Metro Manila college students who prefer the
taste of Papsi Cola is ²/₃(p = ²/₃)
H1 : The proportion of Metro Manila college students who prefer the
taste of Papsi Cola is less than ²/₃(p < ²/₃).
4) Ho: The proportion of TV viewers who watch talk shows from 9:00 to
10:00 in the evening is the same on Wednesday and Fridays (p1 = p2)
H1 : The proportion of TV viewers who watch talk shows from 9:00 to
10:00 in the evening is greater on Wednesday than on Fridays (p1 > p2).

Two types of Errors
• Four possibilities on the Acceptance and
Rejection of a Ho: Consequences of Decisions
in Testing Hypothesis
DECISION/FACT Ho is TRUE Ho is FALSE
ACCEPT Ho: CORRECT DECISION TYPE 2 ERROR denoted by β
TYPE 1 ERROR
REJECT Ho: CORRECT DECISION
denoted by α

P (Type 1 Error)
α
P(Rejecting Ho when Ho is TRUE)
P(Type 2 Error)
β
P(Not Rejecting Ho when Ho is FALSE)

Elements of a Test of a Hypothesis
• Null Hypothesis (Ho)
• Alternative Hypothesis (H1)
• Test Statistic: A sample statistic used to decide
whether to reject the null hypothesis
• Rejection Region
• Calculation of Test Statistic
• Conclusion: Numerical Value falls in the
Rejection Region or not

Level of Significance
• To specify the Probability of committing a Type 1
Error, α, which is popularly known as the Level
of Significance
• We can determine the Critical Values which
define the:
– Region of Rejection (or Critical Region) and
– Region of Acceptance
• The Critical Value serves as the basis for either
Accepting or Rejecting a Hypothesis.
• When α = .05, the Region of Rejection is 0.05 and the
Region of Acceptance is 0.95

One-Tailed and Two Tailed Tests
• Where H1 is Directional, One-Tailed Test
• Where H1 is Non-Directional, Two-Tailed Test
TYPE OF TESTS DIFFERENCE
Region of Rejection lies entirely in one end of the distribution.
One-Tailed Test
Hypothesizing a Range of Values
Involves a Critical Region which is split into two equal parts
Two Tailed Test placed in each tail of the distribution. A value of the parameter
is being hypothesized.

Mathematical Formulation of H1 Region of Rejection
Area of Rejection is placed entirely in
Greater Than ( >)
the Right Tail of the Distribution
Less Than ( < ) Region of Rejection is in the Left Tail
Both Tails contain Equal areas serving as
Not Equal To (≠)
Critical Regions

Example: What form of Hypothesis
Should be Used
• A civic organization is conducting a study to
determine whether the proportion of women
who smoke has increased since last study.
• A garment θmanufacturer of heart attack that that
suspects
Let Let θthe the average of women who smoke
be be proportion age
during the last study
average order size for units of men’s
Therefore,
H : θTherefore,
o = 45
underwear has decreased θ H : θ ≠ 45 H : θ = from last year’s.
1 o o
1 oH:θ>θ
• A doctor claims thatsize for average age of heart
Let θ be the average order the units of men’s
underwear last year
attack patient is 45.
Therefore,
Ho: θ = θo
H1: θ < θo

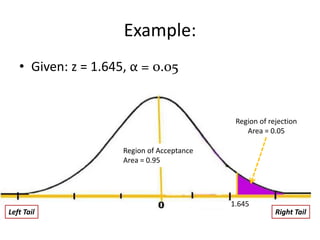
Example:
• Given: z = 1.645, α = 0.05

Region of rejection
Area = 0.05

Region of Acceptance
Area = 0.95

1.645
Left Tail Right Tail

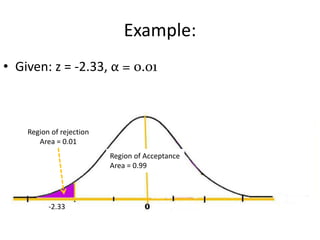
Example:
• Given: z = -2.33, α = 0.01

Region of rejection
Area = 0.01
Area = 0.99

-2.33

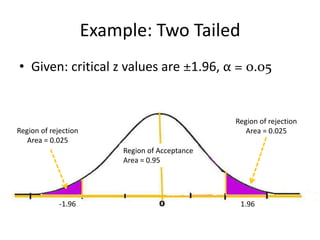
Example: Two Tailed
• Given: critical z values are ±1.96, α = 0.05

Region of rejection
Region of rejection Area = 0.025
Area = 0.025
Area = 0.95

-1.96 1.96

Critical Regions In Testing Hypothesis
• Rejecting Ho

Level of Significance Type of Test One-Tailed Two-Tailed
Computed value of z is GREATER
z > zo z > zo
than the Critical Value
Reject Ho
Computed value of z is LESS than
z < - zo z < -zo
the Negative Critical Value

Steps in Hypothesis Testing

1) Formulate the Ho and the H1
2) Specify the level of significance α
3) Choose the appropriate test statistic
4) Establish the critical region
5) Compute for the value of the statistical test
6) Make a decision and, if possible, draw a
conclusion

Test Concerning Means
(from normally distributed data)
OUTLINE
I. One Sample Test (One Population)
A. σ2 is known (assume that the population variance
is known)
B. σ2 is unknown (the population variance is unknown)

II. Two Sample Test (One Population)

2 2
A. σ1 and σ2 are known
B. σ1 = σ2 = σ2 are unknown
2 2

C. k sample test

(from normally distributed data
I. One Sample Test (One Population)
A. σ2 is known (assume that the population variance is known)

Conditions: We hypothesized that the MEAN of a Normal Population with a
variance of σ2 is µo . We take a random sample of size n from
this population and obtain a sample mean of which is
somewhat different from µo .
To determine whether or not the observed difference
between the computed value and the hypothesized µo is
significant, we formulate the following hypothesis.

1) Ho: µ = µo 2) Ho: µ = µo 3) Ho: µ = µo
H1 : µ < µo H1 : µ ≠ µo H1 : µ >µo

A. σ2 known (assume that the population variance is known)
Since the parameter σ is known, the Z statistics is
employed as the test statistics. Consequently, the z
score corresponding to is:
x  o
z
x
where the denominator σx represents the standard error of the
mean ( or the standard deviation of the sampling distribution of the
mean) and is computed by the formula:

 
Supposed α = 0.05 and the critical values are
x 1.96 and -1.96 then the ff decision rules applies:
n 1. Reject Ho and accept H1, if z > 1.96 or z < -1.96
2. Cannot reject Ho (Accept H1), if z is within
the interval between -1.96 and 1.96


Rejection Region:

Z   Z Z  Z Z  Z
2

Z  Z
2

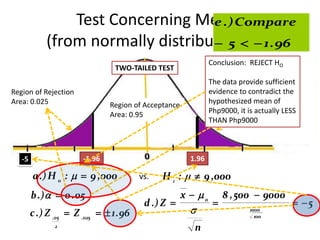
e .) Compare
(from normally distributed   1 . 96
 5 data
Conclusion: REJECT HO
TWO-TAILED TEST
The data provide sufficient
Example: One community college hypothesized that theRegion of Rejection the
Region of Rejection evidence starting monthly
mean to contradict
Area: 0.025 of its graduatesRegion of Acceptance Area: 0.025
hypothesized mean of
salary is Php9000 and a stand deviation of Php1,000. A
Php9000, it is actually LESS
sample of 100 graduates were questioned and it was found that the average
Area: 0.95
THAN Php9000
starting salary is Php8,500.00. Test this hypothesis at 5% level of significance.

Given: µo = 9,000 σ = 1,000 n = 100 x  8 , 500
-5 -1.96 1.96

a .) H o :   9 ,000 vs. H 1 :   9 ,000
b .)   0 . 05 x   o 8 , 500  9000
d .) Z    5
c .) Z .05  Z .025   1 . 96  1000
100
2 n

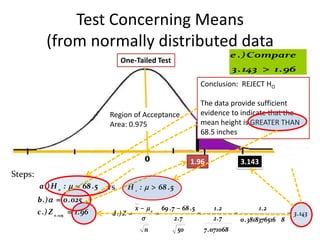
e .) Compare
One-Tailed Test
3 . 143  1 . 96
Region of Rejection
Example: The average height of males in the freshmen class of a certain college
Area: 0.025
The data provide sufficient
has been 68.5 inches, with a standard deviation of 2.7 inches. Is there a
reason to believe thatRegion has been an increase in theto indicateheight if a
there of Acceptance evidence average that the
random sample of 50 Area: 0.975 present freshmen heighthave an average
males in the mean class is GREATER THAN
68.5 inches
height 69.7 inches? Test at 0.025 level of significance.

Given: µo = 68.5 σ= 2.7 x  69 . 7 1.96 3.143
Steps:
a .) H o :   68 . 5 vs. H 1 :   68 . 5
b .)   0 . 025
x   o 69 . 7  68 . 5 1.2 1.2
c .) Z 0 .025  1 . 96 d .) Z      3 . 143
 2 .7 2 .7 0 . 3818376516 8
n 50 7 . 071068

When the population standard deviation σ is unknown and the
sample size n is less than 30, the T statistic is appropriate. The t
value corresponding to a mean x of a sample taken from a
normal population is
x
t
sx
With df = n – 1, where s x 
s
 estimated standard error of the
n
sampling distribution x . Thus, to test the hypothesis µ=µo against
any suitable alternative when σ is unknown and n < 30,
x  o
t  With df = n -1
s
n

Rejection Region:

T   t  ,( n  1 ) T   t T  t  ,( n  1 )
,( n  1 )
2

T  t
,( n  1 )
2

One-Tailed Test e .) Compare
 3 . 06   2 . 821
Example: A major car manufacturer wants to test a new engine to see whether it meets new air
pollution standards. The mean µ of all engines of this type must be less than 20 parts
Region million of carbon. Ten engines are manufactured for testing purposes, and the
per of Rejection
Area: 0.01and standard deviation of the emission for this sample of engines were
mean The data provide sufficient
determined to be: evidence that the engine type
Area: 0.99 meets pollution control
x  17 . 1 parts / million s = 3.0 parts/million

Do the data supply evidence to allow the manufacturer to conclude that this type of engine
meets the pollution standard? Assume that the manufacturer is willing to risk a Type 1
-3.06 with -2.821
error probability α = 0.01.

Given: µo = 20 n = 10 x  17 . 1 s = 3.0

a .) H o :   20 vs . H 1 :   20
b .)   0 . 01
x   0 17 . 1  20
c .) t  ,( n  1 )  t 0 .01 ,( 10  1 )  t 0 .01 , 9   2 . 821 d .) T     3 . 06
s 3 .0
n 10

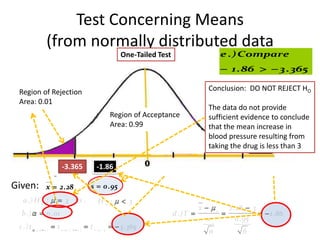
One-Tailed Test e .) Compare
B. σ2 is unknown (the population variance is unknown)1 . 86
   3 . 365
Example: Suppose a pharmaceutical company must demonstrate
that a prescribed dose of a certain new drug DO NOT REJECTinO
Region of Rejection Conclusion: will result H
average increase in blood pressure of lessThe data3do not provide
Area: 0.01 than points. Assume
that only six patients can Acceptance in the sufficientphase of human
Region of be used initial evidence to conclude
n  x  (  x ) Area:(0.99 35 . 79 )  187 . 69 214 . 74  187 . 69
2 2
6 )(
s  testing. Result: the six patients have blood pressureincrease in of
 that  mean increase
the
1.7, 3.0,  1 ) 3.4, 2.7, and 2.1 points. Use the resulting from
n ( n 0.8, 30 30
blood pressure results to
determine if there is evidence that the taking the drugsatisfies the
27 . 05 new drug is less than 3
s  requirement .that the resulting increase in blood pressure
 0 901666 0 . 95
30 -3.365 -1.86
averages less than 3 points.
Given: x  2 .28 s  0 . 95
a .) H o :   3 vs . H0 :   3
x   0 2 . 28  3
b .)   0 . 01 d .) T     1 . 86
s 0 . 95
c .) t  ,( n  1 )  t 0 .01 ,( 6  1 )  t 0 .01 , 5   3 . 365
n 6

Test on the difference in Means

A. σ2 and σ2 are known
1
2

1) Ho: µ1-µ2 = µo 2) Ho: µ1-µ2 = µo 3) Ho: µ1-µ2 = µo
H1 : µ1-µ2 < µo H1 : µ1-µ2 ≠ µo H1 : µ1-µ2 >µo

Test Statistic:
( x 1  x 2 )  o
Z 
1 2
2 2


n1 n2

Rejection Region:

Z   z Z   z Z  z
2

Z  z
Note:
i. µo = 0 2
ii.µ1 - µ2 < µ0 µ1 < µ2, µ2 > µ1
iii.µ1 - µ2 > µo µ1 > µ2, µ2 < µ1

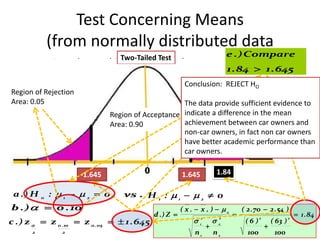
Two-Tailed Test e .) Compare
1 . 84  1 . 645
Example: A university investigation, conducted to determineConclusion: ownership if students affect
whether car REJECT H
O
their academic achievement, was based on two random samples Regionstudents, each drawn
of 100 of Rejection
Region of the student body. The average and standard deviation of each group’s GPA (grade point
from Rejection
Area:average) are as shown.
0.05 Area: 0.05
The data provide sufficient evidence to
Region of Acceptance indicate a difference in the mean
Non-Car owners (n1=100) Car Owners (n2=100)
Area: 0.90 achievement between car owners and
GPA GPA
non-car owners, in fact non car owners
x 1  2 . 70 s  0 . 60 2 . 54 s  0 . performance than
x 2  have better academic63
1 2
car owners.
Do the data present sufficient evidence to indicate a difference in the mean achievement between car
owners and noncar owners? Test using α=0.10

-1.645 1.645 1.84
Define: µ1 = mean GPA for Non-car owners; µ2 = mean GPA for Car owners; µ0 = 0

a .) H 0
: 1  2  0 vs . H 1 :  1   2  0
b .)   0 . 10 ( x 1  x 2 )  0 ( 2 . 70  2 . 54 )
d .) Z    1 . 84
c .) z   z 0 . 10  z 0 . 05   1 . 645 1 2
2 2 2 2
(6) ( 63 )
 
2 2 n1 n2 100 100


1
2

1) Ho: µ1-µ2 = µo 2) Ho: µ1-µ2 = µo 3) Ho: µ1-µ2 = µo
H1 : µ1-µ2 < µo H1 : µ1-µ2 ≠ µo H1 : µ1-µ2 >µo

Test Statistic:
( n 1  1 )s 1  ( n 2  1 )s 2
2 2
( x 1  x 2 )  o where S p 
T  n1  n2  2
1 1
Sp 
n1 n2


1
2

Rejection Region:

T   t  ,( n 1  n 2  2 ) T   t T  t  ,( n 1  n 2  2 )
,( n 1  n 2  2 )
2

T  t
,( n 1  n 2  2 )
2

2 2

Example: A television network wanted to determine whether sports events
or first run movies attract more viewers in the prime-time hours. It
selected 28 prime-time evenings; of these, 13 had programs
devoted to major sports events and the remaining 15 had first –
run. The number of viewers (estimated by a television viewer
rating firm) was reported for each program. If µ1 is the mean
number of sports viewers per evening and µ2 is the mean number
of movie viewers per evening, is there a difference in the mean
number of viewers at 0.05 level of significance?

The TV network’s samples produce the results below:

Sports: n1 = 13 s1 = 1.8 million x 1  6 . 8 million
Movies: n2 = 15 s2 = 1.6 million x 2  5 . 3 million

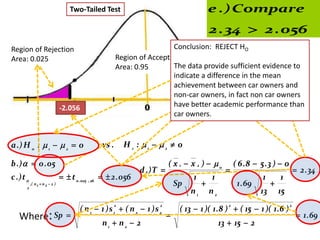
Two-Tailed Test e .) Compare
2 . 34  2 . 056
Region of Rejection Conclusion: REJECT HO
Region of Acceptance Region of Rejection
Area: 0.025
Area: 0.95 Area: 0.025
The data provide sufficient evidence to
indicate a difference in the mean
achievement between car owners and
non-car owners, in fact non car owners
-2.056 have better academic performance than
2.056 2.34
car owners.

a .) H o :  1   2  0 vs . H 1 : 1  2  0

b .)   0 . 05 ( x 1  x 2 )  0 ( 6 .8  5 .3 )  0
d .) T    2 . 34
c .) t    t 0 .025 , 26   2 . 056 1 1 1 1
2
,( n 1  n 2  2 ) Sp  1 . 69 
n1 n2 13 15

( n 1  1 )s1  ( n 2  1 )s 2 ( 13  1 )( 1 . 8 )  ( 15  1 )( 1 . 6 )
2 2 2 2

Where: Sp    1 . 69
n1  n2  2 13  15  2

STATISTICS: Hypothesis Testing

Recommended

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to STATISTICS: Hypothesis Testing (20)

More from jundumaug1 (20)

Recently uploaded (20)

STATISTICS: Hypothesis Testing

Editor's Notes