businessstatistics-stat10022-200411201812.ppt
Download as ppt, pdf0 likes13 views
Business statistics ppt
1 of 21
Download to read offline













Ad
Recommended
Basics of statistics by Arup Nama Das



Basics of statistics by Arup Nama DasArup8 This document provides an overview of biostatistics, including definitions, concepts, and methods. It defines statistics as the science of collecting, organizing, summarizing, analyzing, and interpreting data. Various statistical concepts are explained, such as variables, distributions, frequency distributions, measures of center and variability. Graphical and numerical methods for presenting data are described, including histograms, box plots, mean, median, and standard deviation. Methods for summarizing categorical and numerical variable data are also outlined.
presentation



presentationPwalmiki This document provides an overview of basic statistics concepts. It defines statistics as the science of collecting, analyzing, and interpreting data. There are two main types of statistics: descriptive statistics which summarize data, and inferential statistics which make predictions from data. Key concepts discussed include variables, frequency distributions, measures of center such as mean and median, measures of variability such as range and standard deviation, and methods of presenting data graphically and numerically.
Student’s presentation



Student’s presentationPwalmiki This document provides an overview of basic statistics concepts. It defines statistics as the science of collecting, analyzing, and interpreting data. There are two main types of statistics: descriptive statistics which summarize data, and inferential statistics which make predictions from data. Key concepts discussed include variables, frequency distributions, measures of center such as mean and median, measures of variability such as range and standard deviation, and methods of presenting data graphically and numerically.
STATISTICAL PROCEDURES (Discriptive Statistics).pptx



STATISTICAL PROCEDURES (Discriptive Statistics).pptxMuhammadNafees42 This document discusses statistical procedures and their applications. It defines key statistical terminology like population, sample, parameter, and variable. It describes the two main types of statistics - descriptive and inferential statistics. Descriptive statistics summarize and describe data through measures of central tendency (mean, median, mode), dispersion, frequency, and position. The mean is the average value, the median is the middle value, and the mode is the most frequent value in a data set. Descriptive statistics help understand the characteristics of a sample or small population.
Data Presentation and Slide Preparation



Data Presentation and Slide PreparationAchu dhan Data:
A set of values recorded on one or more observational units i.e. Object, person etc
Types of data:
Qualitative/ Quantitative data
Discrete/ Continuous data
Primary/ Secondary data
Nominal/ Ordinal data
General Statistics boa



General Statistics boaraileeanne The document contains an outline of the table of contents for a textbook on general statistics. It covers topics such as preliminary concepts, data collection and presentation, measures of central tendency, measures of dispersion and skewness, and permutations and combinations. Sample chapters discuss introduction to statistics, variables and data, methods of presenting data through tables, graphs and diagrams, computing the mean, median and mode, and other statistical measures.
Statistics final seminar



Statistics final seminarTejas Jagtap This document provides an introduction to statistics, including what statistics is, who uses it, and different types of variables and data presentation. Statistics is defined as collecting, organizing, analyzing, and interpreting numerical data to assist with decision making. Descriptive statistics organizes and summarizes data, while inferential statistics makes estimates or predictions about populations based on samples. Variables can be qualitative or quantitative, and quantitative variables can be discrete or continuous. Data can be presented through frequency tables, graphs like histograms and polygons, and cumulative frequency distributions.
EDUCATIONAL STATISTICS_Unit_I.ppt



EDUCATIONAL STATISTICS_Unit_I.pptSasi Kumar The document discusses descriptive statistics and various statistical concepts. It covers measures of central tendency like mean, median and mode. It also discusses measures of variability/dispersion such as range, mean deviation and standard deviation. Additionally, it covers different scales of measurement like nominal, ordinal, interval and ratio scales. Finally, it discusses various methods of graphical representation of data like pie charts, bar graphs, histograms and frequency polygons. The key aspects of each concept are defined along with examples.
Class1.ppt



Class1.pptGautam G The document provides an overview of the structure and content of a biostatistics class. It includes:
- Two instructors who will teach 8 classes, with 3 take-home assignments and a final exam.
- Default and contributed datasets that students can use, focusing on nominal, ordinal, interval, and ratio variables.
- Optional late topics like microarray analysis, pattern recognition, and time series analysis.
Class1.ppt



Class1.pptPerumalPitchandi The class consists of 8 classes taught by two instructors over biostatistics and psychology. There are 3 take-home assignments due in classes 3, 5, and 7 and a final take-home exam assigned in class 8. The default dataset for class participation contains data on 60 subjects across 3-4 treatment groups and various measure types. Special topics may include microarray analysis, pattern recognition, machine learning, and hidden Markov modeling.
Class1.ppt



Class1.pptSandeepkumar628916 The document provides an overview of the structure and content of a biostatistics class. It includes:
- Two instructors who will teach 8 classes, with 3 take-home assignments and a final exam.
- Default datasets with health data that students can use for assignments, and an option for students to bring their own de-identified data.
- Possible special topics like machine learning, time series analysis, and others.
Introduction to Statistics - Basics of Data - Class 1



Introduction to Statistics - Basics of Data - Class 1RajnishSingh367990 The document provides an overview of the structure and content of a biostatistics class. It includes:
- Two instructors who will teach 8 classes, with 3 take-home assignments and a final exam.
- Default and contributed datasets that students can use, focusing on nominal, ordinal, interval, and ratio variables.
- Optional late topics like microarray analysis, pattern recognition, and time series analysis.
- A taxonomy of statistics, covering statistical description, presentation of data through graphs and numbers, and measures of center and variability.
Class1.ppt



Class1.ppthanreaz219 The class consists of 8 classes taught by two instructors over biostatistics and psychology. There are 3 take-home assignments due in classes 3, 5, and 7. A final take-home exam is assigned in class 8. The default dataset contains data on 60 subjects across 3-4 treatment groups with various measure types. Students can also bring their own de-identified datasets. The course covers topics like microarray analysis, pattern recognition, machine learning and more.
STATISTICS BASICS INCLUDING DESCRIPTIVE STATISTICS



STATISTICS BASICS INCLUDING DESCRIPTIVE STATISTICSnagamani651296 The class consists of 8 classes taught by two instructors over biostatistics and psychology. There are 3 take-home assignments due in classes 3, 5, and 7. A final take-home exam is assigned in class 8. The default dataset contains data on 60 subjects across 3-4 treatment groups with various measure types. Students can also bring their own de-identified datasets. The course covers topics like microarray analysis, pattern recognition, machine learning and more.
Statistics



StatisticsDeepanshu Sharma The class consists of 8 classes taught by two instructors. There are 3 take-home assignments due in classes 3, 5, and 7. A final take-home exam is assigned in class 8. The default dataset contains data from 60 subjects across 3-4 groups with different variable types. Students can also bring their own de-identified datasets. Special topics may include microarray analysis, pattern recognition, machine learning, and time series analysis.
Statistics as a discipline



Statistics as a disciplineRosalinaTPayumo Statistics is the collection, organization, analysis, and presentation of data. It has become important for professionals, scientists, and citizens to make sense of large amounts of data. Statistics are used across many disciplines from science to business. There are two main types of statistical methods - descriptive statistics which summarize data through measures like the mean and median, and inferential statistics which make inferences about populations based on samples. Descriptive statistics describe data through measures of central tendency and variability, while inferential statistics allow inferences to be made from samples to populations through techniques like hypothesis testing.
Statistics



Statisticspikuoec This document provides an overview of key concepts in statistics including:
- Descriptive statistics such as frequency distributions which organize and summarize data
- Inferential statistics which make estimates or predictions about populations based on samples
- Types of variables including quantitative, qualitative, discrete and continuous
- Levels of measurement including nominal, ordinal, interval and ratio
- Common measures of central tendency (mean, median, mode) and dispersion (range, standard deviation)
Standerd Deviation and calculation.pdf



Standerd Deviation and calculation.pdfNJJAISWALPC This document discusses different types of data and methods for presenting data. It describes qualitative and quantitative data, discrete and continuous data, and primary and secondary data. It also covers nominal and ordinal data. Common methods for presenting data include tabulation, bar charts, histograms, frequency polygons, cumulative frequency diagrams, scatter diagrams, line diagrams, and pie charts. The document provides guidelines for constructing tables and various chart types to clearly present data in a way that facilitates analysis and understanding.
presentation of data



presentation of dataShafeek S This document discusses different types of data and methods for presenting data. It describes qualitative and quantitative data, discrete and continuous data, and primary and secondary data. It also covers nominal and ordinal data. Common methods for presenting data include tabulation and various charts or diagrams. Tabulation involves organizing data into tables, following specific rules. Charts allow visualization of data and include bar charts, histograms, frequency polygons, cumulative frequency diagrams, scatter diagrams, line diagrams, and pie charts. Each chart has specific purposes and guidelines for effective presentation of data.
Biostatistics



BiostatisticsDr. Senthilvel Vasudevan - Biostatistics refers to applying statistical methods to biological and medical problems. It is also called biometrics, which means biological measurement or measurement of life.
- There are two main types of statistics: descriptive statistics which organizes and summarizes data, and inferential statistics which allows conclusions to be made from the sample data.
- Data can be qualitative like gender or eye color, or quantitative which has numerical values like age, height, weight. Quantitative data can further be interval/ratio or discrete/continuous.
- Common measures of central tendency include the mean, median and mode. Measures of variability include range, standard deviation, variance and coefficient of variation.
- Correlation describes the relationship between two variables
STATISTICS.pptx for the scholars and students



STATISTICS.pptx for the scholars and studentsssuseref12b21 The document provides an overview of statistics, including definitions, types, and key concepts. It defines statistics as the science of collecting, presenting, analyzing, and interpreting data. It discusses descriptive statistics, which summarize and organize raw data, and inferential statistics, which allow generalization from samples to populations. The document also covers variables, scales of measurement, measures of central tendency (mean, median, mode), measures of dispersion (range, standard deviation), and other statistical terminology.
Interfacing PMW3901 Optical Flow Sensor with ESP32



Interfacing PMW3901 Optical Flow Sensor with ESP32CircuitDigest Learn how to connect a PMW3901 Optical Flow Sensor with an ESP32 to measure surface motion and movement without GPS! This project explains how to set up the sensor using SPI communication, helping create advanced robotics like autonomous drones and smart robots.
Introduction to FLUID MECHANICS & KINEMATICS



Introduction to FLUID MECHANICS & KINEMATICSnarayanaswamygdas Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasmas) and the forces on them. Originally applied to water (hydromechanics), it found applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical, and biomedical engineering, as well as geophysics, oceanography, meteorology, astrophysics, and biology.
It can be divided into fluid statics, the study of various fluids at rest, and fluid dynamics.
Fluid statics, also known as hydrostatics, is the study of fluids at rest, specifically when there's no relative motion between fluid particles. It focuses on the conditions under which fluids are in stable equilibrium and doesn't involve fluid motion.
Fluid kinematics is the branch of fluid mechanics that focuses on describing and analyzing the motion of fluids, such as liquids and gases, without considering the forces that cause the motion. It deals with the geometrical and temporal aspects of fluid flow, including velocity and acceleration. Fluid dynamics, on the other hand, considers the forces acting on the fluid.
Fluid dynamics is the study of the effect of forces on fluid motion. It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a macroscopic viewpoint rather than from microscopic.
Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems are partly or wholly unsolved and are best addressed by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics (CFD), is devoted to this approach. Particle image velocimetry, an experimental method for visualizing and analyzing fluid flow, also takes advantage of the highly visual nature of fluid flow.
Fundamentally, every fluid mechanical system is assumed to obey the basic laws :
Conservation of mass
Conservation of energy
Conservation of momentum
The continuum assumption
For example, the assumption that mass is conserved means that for any fixed control volume (for example, a spherical volume)—enclosed by a control surface—the rate of change of the mass contained in that volume is equal to the rate at which mass is passing through the surface from outside to inside, minus the rate at which mass is passing from inside to outside. This can be expressed as an equation in integral form over the control volume.
The continuum assumption is an idealization of continuum mechanics under which fluids can be treated as continuous, even though, on a microscopic scale, they are composed of molecules. Under the continuum assumption, macroscopic (observed/measurable) properties such as density, pressure, temperature, and bulk velocity are taken to be well-defined at "infinitesimal" volume elements—small in comparison to the characteristic length scale of the system, but large in comparison to molecular length scale
Ad
More Related Content
Similar to businessstatistics-stat10022-200411201812.ppt (20)
Statistics final seminar



Statistics final seminarTejas Jagtap This document provides an introduction to statistics, including what statistics is, who uses it, and different types of variables and data presentation. Statistics is defined as collecting, organizing, analyzing, and interpreting numerical data to assist with decision making. Descriptive statistics organizes and summarizes data, while inferential statistics makes estimates or predictions about populations based on samples. Variables can be qualitative or quantitative, and quantitative variables can be discrete or continuous. Data can be presented through frequency tables, graphs like histograms and polygons, and cumulative frequency distributions.
EDUCATIONAL STATISTICS_Unit_I.ppt



EDUCATIONAL STATISTICS_Unit_I.pptSasi Kumar The document discusses descriptive statistics and various statistical concepts. It covers measures of central tendency like mean, median and mode. It also discusses measures of variability/dispersion such as range, mean deviation and standard deviation. Additionally, it covers different scales of measurement like nominal, ordinal, interval and ratio scales. Finally, it discusses various methods of graphical representation of data like pie charts, bar graphs, histograms and frequency polygons. The key aspects of each concept are defined along with examples.
Class1.ppt



Class1.pptGautam G The document provides an overview of the structure and content of a biostatistics class. It includes:
- Two instructors who will teach 8 classes, with 3 take-home assignments and a final exam.
- Default and contributed datasets that students can use, focusing on nominal, ordinal, interval, and ratio variables.
- Optional late topics like microarray analysis, pattern recognition, and time series analysis.
Class1.ppt



Class1.pptPerumalPitchandi The class consists of 8 classes taught by two instructors over biostatistics and psychology. There are 3 take-home assignments due in classes 3, 5, and 7 and a final take-home exam assigned in class 8. The default dataset for class participation contains data on 60 subjects across 3-4 treatment groups and various measure types. Special topics may include microarray analysis, pattern recognition, machine learning, and hidden Markov modeling.
Class1.ppt



Class1.pptSandeepkumar628916 The document provides an overview of the structure and content of a biostatistics class. It includes:
- Two instructors who will teach 8 classes, with 3 take-home assignments and a final exam.
- Default datasets with health data that students can use for assignments, and an option for students to bring their own de-identified data.
- Possible special topics like machine learning, time series analysis, and others.
Introduction to Statistics - Basics of Data - Class 1



Introduction to Statistics - Basics of Data - Class 1RajnishSingh367990 The document provides an overview of the structure and content of a biostatistics class. It includes:
- Two instructors who will teach 8 classes, with 3 take-home assignments and a final exam.
- Default and contributed datasets that students can use, focusing on nominal, ordinal, interval, and ratio variables.
- Optional late topics like microarray analysis, pattern recognition, and time series analysis.
- A taxonomy of statistics, covering statistical description, presentation of data through graphs and numbers, and measures of center and variability.
Class1.ppt



Class1.ppthanreaz219 The class consists of 8 classes taught by two instructors over biostatistics and psychology. There are 3 take-home assignments due in classes 3, 5, and 7. A final take-home exam is assigned in class 8. The default dataset contains data on 60 subjects across 3-4 treatment groups with various measure types. Students can also bring their own de-identified datasets. The course covers topics like microarray analysis, pattern recognition, machine learning and more.
STATISTICS BASICS INCLUDING DESCRIPTIVE STATISTICS



STATISTICS BASICS INCLUDING DESCRIPTIVE STATISTICSnagamani651296 The class consists of 8 classes taught by two instructors over biostatistics and psychology. There are 3 take-home assignments due in classes 3, 5, and 7. A final take-home exam is assigned in class 8. The default dataset contains data on 60 subjects across 3-4 treatment groups with various measure types. Students can also bring their own de-identified datasets. The course covers topics like microarray analysis, pattern recognition, machine learning and more.
Statistics



StatisticsDeepanshu Sharma The class consists of 8 classes taught by two instructors. There are 3 take-home assignments due in classes 3, 5, and 7. A final take-home exam is assigned in class 8. The default dataset contains data from 60 subjects across 3-4 groups with different variable types. Students can also bring their own de-identified datasets. Special topics may include microarray analysis, pattern recognition, machine learning, and time series analysis.
Statistics as a discipline



Statistics as a disciplineRosalinaTPayumo Statistics is the collection, organization, analysis, and presentation of data. It has become important for professionals, scientists, and citizens to make sense of large amounts of data. Statistics are used across many disciplines from science to business. There are two main types of statistical methods - descriptive statistics which summarize data through measures like the mean and median, and inferential statistics which make inferences about populations based on samples. Descriptive statistics describe data through measures of central tendency and variability, while inferential statistics allow inferences to be made from samples to populations through techniques like hypothesis testing.
Statistics



Statisticspikuoec This document provides an overview of key concepts in statistics including:
- Descriptive statistics such as frequency distributions which organize and summarize data
- Inferential statistics which make estimates or predictions about populations based on samples
- Types of variables including quantitative, qualitative, discrete and continuous
- Levels of measurement including nominal, ordinal, interval and ratio
- Common measures of central tendency (mean, median, mode) and dispersion (range, standard deviation)
Standerd Deviation and calculation.pdf



Standerd Deviation and calculation.pdfNJJAISWALPC This document discusses different types of data and methods for presenting data. It describes qualitative and quantitative data, discrete and continuous data, and primary and secondary data. It also covers nominal and ordinal data. Common methods for presenting data include tabulation, bar charts, histograms, frequency polygons, cumulative frequency diagrams, scatter diagrams, line diagrams, and pie charts. The document provides guidelines for constructing tables and various chart types to clearly present data in a way that facilitates analysis and understanding.
presentation of data



presentation of dataShafeek S This document discusses different types of data and methods for presenting data. It describes qualitative and quantitative data, discrete and continuous data, and primary and secondary data. It also covers nominal and ordinal data. Common methods for presenting data include tabulation and various charts or diagrams. Tabulation involves organizing data into tables, following specific rules. Charts allow visualization of data and include bar charts, histograms, frequency polygons, cumulative frequency diagrams, scatter diagrams, line diagrams, and pie charts. Each chart has specific purposes and guidelines for effective presentation of data.
Biostatistics



BiostatisticsDr. Senthilvel Vasudevan - Biostatistics refers to applying statistical methods to biological and medical problems. It is also called biometrics, which means biological measurement or measurement of life.
- There are two main types of statistics: descriptive statistics which organizes and summarizes data, and inferential statistics which allows conclusions to be made from the sample data.
- Data can be qualitative like gender or eye color, or quantitative which has numerical values like age, height, weight. Quantitative data can further be interval/ratio or discrete/continuous.
- Common measures of central tendency include the mean, median and mode. Measures of variability include range, standard deviation, variance and coefficient of variation.
- Correlation describes the relationship between two variables
STATISTICS.pptx for the scholars and students



STATISTICS.pptx for the scholars and studentsssuseref12b21 The document provides an overview of statistics, including definitions, types, and key concepts. It defines statistics as the science of collecting, presenting, analyzing, and interpreting data. It discusses descriptive statistics, which summarize and organize raw data, and inferential statistics, which allow generalization from samples to populations. The document also covers variables, scales of measurement, measures of central tendency (mean, median, mode), measures of dispersion (range, standard deviation), and other statistical terminology.
Recently uploaded (20)
Interfacing PMW3901 Optical Flow Sensor with ESP32



Interfacing PMW3901 Optical Flow Sensor with ESP32CircuitDigest Learn how to connect a PMW3901 Optical Flow Sensor with an ESP32 to measure surface motion and movement without GPS! This project explains how to set up the sensor using SPI communication, helping create advanced robotics like autonomous drones and smart robots.
Introduction to FLUID MECHANICS & KINEMATICS



Introduction to FLUID MECHANICS & KINEMATICSnarayanaswamygdas Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasmas) and the forces on them. Originally applied to water (hydromechanics), it found applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical, and biomedical engineering, as well as geophysics, oceanography, meteorology, astrophysics, and biology.
It can be divided into fluid statics, the study of various fluids at rest, and fluid dynamics.
Fluid statics, also known as hydrostatics, is the study of fluids at rest, specifically when there's no relative motion between fluid particles. It focuses on the conditions under which fluids are in stable equilibrium and doesn't involve fluid motion.
Fluid kinematics is the branch of fluid mechanics that focuses on describing and analyzing the motion of fluids, such as liquids and gases, without considering the forces that cause the motion. It deals with the geometrical and temporal aspects of fluid flow, including velocity and acceleration. Fluid dynamics, on the other hand, considers the forces acting on the fluid.
Fluid dynamics is the study of the effect of forces on fluid motion. It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a macroscopic viewpoint rather than from microscopic.
Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems are partly or wholly unsolved and are best addressed by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics (CFD), is devoted to this approach. Particle image velocimetry, an experimental method for visualizing and analyzing fluid flow, also takes advantage of the highly visual nature of fluid flow.
Fundamentally, every fluid mechanical system is assumed to obey the basic laws :
Conservation of mass
Conservation of energy
Conservation of momentum
The continuum assumption
For example, the assumption that mass is conserved means that for any fixed control volume (for example, a spherical volume)—enclosed by a control surface—the rate of change of the mass contained in that volume is equal to the rate at which mass is passing through the surface from outside to inside, minus the rate at which mass is passing from inside to outside. This can be expressed as an equation in integral form over the control volume.
The continuum assumption is an idealization of continuum mechanics under which fluids can be treated as continuous, even though, on a microscopic scale, they are composed of molecules. Under the continuum assumption, macroscopic (observed/measurable) properties such as density, pressure, temperature, and bulk velocity are taken to be well-defined at "infinitesimal" volume elements—small in comparison to the characteristic length scale of the system, but large in comparison to molecular length scale
SICPA: Fabien Keller - background introduction



SICPA: Fabien Keller - background introductionfabienklr Dear SICPA Team,
Please find attached a document outlining my professional background and experience.
I remain at your disposal should you have any questions or require further information.
Best regards,
Fabien Keller
Dynamics of Structures with Uncertain Properties.pptx



Dynamics of Structures with Uncertain Properties.pptxUniversity of Glasgow In modern aerospace engineering, uncertainty is not an inconvenience — it is a defining feature. Lightweight structures, composite materials, and tight performance margins demand a deeper understanding of how variability in material properties, geometry, and boundary conditions affects dynamic response. This keynote presentation tackles the grand challenge: how can we model, quantify, and interpret uncertainty in structural dynamics while preserving physical insight?
This talk reflects over two decades of research at the intersection of structural mechanics, stochastic modelling, and computational dynamics. Rather than adopting black-box probabilistic methods that obscure interpretation, the approaches outlined here are rooted in engineering-first thinking — anchored in modal analysis, physical realism, and practical implementation within standard finite element frameworks.
The talk is structured around three major pillars:
1. Parametric Uncertainty via Random Eigenvalue Problems
* Analytical and asymptotic methods are introduced to compute statistics of natural frequencies and mode shapes.
* Key insight: eigenvalue sensitivity depends on spectral gaps — a critical factor for systems with clustered modes (e.g., turbine blades, panels).
2. Parametric Uncertainty in Dynamic Response using Modal Projection
* Spectral function-based representations are presented as a frequency-adaptive alternative to classical stochastic expansions.
* Efficient Galerkin projection techniques handle high-dimensional random fields while retaining mode-wise physical meaning.
3. Nonparametric Uncertainty using Random Matrix Theory
* When system parameters are unknown or unmeasurable, Wishart-distributed random matrices offer a principled way to encode uncertainty.
* A reduced-order implementation connects this theory to real-world systems — including experimental validations with vibrating plates and large-scale aerospace structures.
Across all topics, the focus is on reduced computational cost, physical interpretability, and direct applicability to aerospace problems.
The final section outlines current integration with FE tools (e.g., ANSYS, NASTRAN) and ongoing research into nonlinear extensions, digital twin frameworks, and uncertainty-informed design.
Whether you're a researcher, simulation engineer, or design analyst, this presentation offers a cohesive, physics-based roadmap to quantify what we don't know — and to do so responsibly.
Key words
Stochastic Dynamics, Structural Uncertainty, Aerospace Structures, Uncertainty Quantification, Random Matrix Theory, Modal Analysis, Spectral Methods, Engineering Mechanics, Finite Element Uncertainty, Wishart Distribution, Parametric Uncertainty, Nonparametric Modelling, Eigenvalue Problems, Reduced Order Modelling, ASME SSDM2025
Prediction of Flexural Strength of Concrete Produced by Using Pozzolanic Mate...



Prediction of Flexural Strength of Concrete Produced by Using Pozzolanic Mate...Journal of Soft Computing in Civil Engineering The use of huge quantity of natural fine aggregate (NFA) and cement in civil construction work which have given rise to various ecological problems. The industrial waste like Blast furnace slag (GGBFS), fly ash, metakaolin, silica fume can be used as partly replacement for cement and manufactured sand obtained from crusher, was partly used as fine aggregate. In this work, MATLAB software model is developed using neural network toolbox to predict the flexural strength of concrete made by using pozzolanic materials and partly replacing natural fine aggregate (NFA) by Manufactured sand (MS). Flexural strength was experimentally calculated by casting beams specimens and results obtained from experiment were used to develop the artificial neural network (ANN) model. Total 131 results values were used to modeling formation and from that 30% data record was used for testing purpose and 70% data record was used for training purpose. 25 input materials properties were used to find the 28 days flexural strength of concrete obtained from partly replacing cement with pozzolans and partly replacing natural fine aggregate (NFA) by manufactured sand (MS). The results obtained from ANN model provides very strong accuracy to predict flexural strength of concrete obtained from partly replacing cement with pozzolans and natural fine aggregate (NFA) by manufactured sand.
最新版加拿大魁北克大学蒙特利尔分校毕业证(UQAM毕业证书)原版定制



最新版加拿大魁北克大学蒙特利尔分校毕业证(UQAM毕业证书)原版定制Taqyea 魁北克大学蒙特利尔分校diploma安全可靠购买【Q微号:1954 292 140】魁北克大学蒙特利尔分校毕业证(UQAM毕业证书)成绩单、offer、学位证、留信学历认证(永久存档真实可查)采用学校原版纸张、特殊工艺完全按照原版一比一制作(包括:隐形水印,阴影底纹,钢印LOGO烫金烫银,LOGO烫金烫银复合重叠,文字图案浮雕,激光镭射,紫外荧光,温感,复印防伪)行业标杆!精益求精,诚心合作,真诚制作!多年品质 ,按需精细制作,24小时接单,全套进口原装设备,十五年致力于帮助留学生解决难题,业务范围有加拿大、英国、澳洲、韩国、美国、新加坡,新西兰等学历材料,包您满意。
【关于学历材料质量】
我们承诺采用的是学校原版纸张(原版纸质、底色、纹路)我们工厂拥有全套进口原装设备,特殊工艺都是采用不同机器制作,仿真度基本可以达到100%,所有成品以及工艺效果都可提前给客户展示,不满意可以根据客户要求进行调整,直到满意为止!
【业务选择办理准则】
一、工作未确定,回国需先给父母、亲戚朋友看下文凭的情况,办理一份就读学校的毕业证魁北克大学蒙特利尔分校毕业证(UQAM毕业证书)【微信号1954 292 140】文凭即可
二、回国进私企、外企、自己做生意的情况,这些单位是不查询毕业证真伪的,而且国内没有渠道去查询国外文凭的真假,也不需要提供真实教育部认证。鉴于此,办理一份毕业证魁北克大学蒙特利尔分校毕业证(UQAM毕业证书)【微信号1954 292 140】即可
三、进国企,银行,事业单位,考公务员等等,这些单位是必需要提供真实教育部认证的,办理教育部认证所需资料众多且烦琐,所有材料您都必须提供原件,我们凭借丰富的经验,快捷的绿色通道帮您快速整合材料,让您少走弯路。
PRIZ Academy - Functional Modeling In Action with PRIZ.pdf



PRIZ Academy - Functional Modeling In Action with PRIZ.pdfPRIZ Guru This PRIZ Academy deck walks you step-by-step through Functional Modeling in Action, showing how Subject-Action-Object (SAO) analysis pinpoints critical functions, ranks harmful interactions, and guides fast, focused improvements. You’ll see:
Core SAO concepts and scoring logic
A wafer-breakage case study that turns theory into practice
A live PRIZ Platform demo that builds the model in minutes
Ideal for engineers, QA managers, and innovation leads who need clearer system insight and faster root-cause fixes. Dive in, map functions, and start improving what really matters.
Process Parameter Optimization for Minimizing Springback in Cold Drawing Proc...



Process Parameter Optimization for Minimizing Springback in Cold Drawing Proc...Journal of Soft Computing in Civil Engineering In tube drawing process, a tube is pulled out through a die and a plug to reduce its diameter and thickness as per the requirement. Dimensional accuracy of cold drawn tubes plays a vital role in the further quality of end products and controlling rejection in manufacturing processes of these end products. Springback phenomenon is the elastic strain recovery after removal of forming loads, causes geometrical inaccuracies in drawn tubes. Further, this leads to difficulty in achieving close dimensional tolerances. In the present work springback of EN 8 D tube material is studied for various cold drawing parameters. The process parameters in this work include die semi-angle, land width and drawing speed. The experimentation is done using Taguchi’s L36 orthogonal array, and then optimization is done in data analysis software Minitab 17. The results of ANOVA shows that 15 degrees die semi-angle,5 mm land width and 6 m/min drawing speed yields least springback. Furthermore, optimization algorithms named Particle Swarm Optimization (PSO), Simulated Annealing (SA) and Genetic Algorithm (GA) are applied which shows that 15 degrees die semi-angle, 10 mm land width and 8 m/min drawing speed results in minimal springback with almost 10.5 % improvement. Finally, the results of experimentation are validated with Finite Element Analysis technique using ANSYS.
2025 Apply BTech CEC .docx



2025 Apply BTech CEC .docxtusharmanagementquot Finding details regarding 2025 Apply BTech CEC. Contact Admission Chanakya at +91-9934656111 /+91-9934613222 (Devanshu Sharma) Website – bangalore-admission.com or email us at contact@admissionchanakya.com
RICS Membership-(The Royal Institution of Chartered Surveyors).pdf



RICS Membership-(The Royal Institution of Chartered Surveyors).pdfMohamedAbdelkader115 Glad to be one of only 14 members inside Kuwait to hold this credential.
Please check the members inside kuwait from this link:
https://www.rics.org/networking/find-a-member.html?firstname=&lastname=&town=&country=Kuwait&member_grade=(AssocRICS)&expert_witness=&accrediation=&page=1
Artificial intelligence and machine learning.pptx



Artificial intelligence and machine learning.pptxrakshanatarajan005 Artificial Intelligence full data
Compiler Design_Intermediate code generation new ppt.pptx



Compiler Design_Intermediate code generation new ppt.pptxRushaliDeshmukh2 Intermediate representations. Syntax tree, Postfix expression, Three address code, ICG for assignment statement, boolean expression
COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf![COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf](https://ckxe7twkl7vq3ljkxejyz-s-a2157.bj.tsgdht.cn/ss_thumbnails/module-02notesbcg402-cgv-250506151048-aef09ce3-thumbnail.jpg?width=560&fit=bounds)
![COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf](https://ckxe7twkl7vq3ljkxejyz-s-a2157.bj.tsgdht.cn/ss_thumbnails/module-02notesbcg402-cgv-250506151048-aef09ce3-thumbnail.jpg?width=560&fit=bounds)
![COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf](https://ckxe7twkl7vq3ljkxejyz-s-a2157.bj.tsgdht.cn/ss_thumbnails/module-02notesbcg402-cgv-250506151048-aef09ce3-thumbnail.jpg?width=560&fit=bounds)
![COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf](https://ckxe7twkl7vq3ljkxejyz-s-a2157.bj.tsgdht.cn/ss_thumbnails/module-02notesbcg402-cgv-250506151048-aef09ce3-thumbnail.jpg?width=560&fit=bounds)
COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdfAlvas Institute of Engineering and technology, Moodabidri 2D and 3D graphics with OpenGL: 2D Geometric Transformations: Basic 2D Geometric Transformations,
matrix representations and homogeneous coordinates, OpenGL raster transformations, Transformation
between 2D coordinate systems,OpenGL geometric transformation functions.
3D Geometric Transformations:3D Translation, rotation, scaling, OpenGL geometric transformations
functions
Compiler Design_Code Optimization tech.pptx



Compiler Design_Code Optimization tech.pptxRushaliDeshmukh2 Criteria for Code-Improving Transformations
Principal Sources of Optimization
Applications of Centroid in Structural Engineering



Applications of Centroid in Structural Engineeringsuvrojyotihalder2006 Applications of Centroid in Structural Engineering
6th International Conference on Big Data, Machine Learning and IoT (BMLI 2025)



6th International Conference on Big Data, Machine Learning and IoT (BMLI 2025)ijflsjournal087 Call for Papers..!!!
6th International Conference on Big Data, Machine Learning and IoT (BMLI 2025)
June 21 ~ 22, 2025, Sydney, Australia
Webpage URL : https://inwes2025.org/bmli/index
Here's where you can reach us : bmli@inwes2025.org (or) bmliconf@yahoo.com
Paper Submission URL : https://inwes2025.org/submission/index.php
Prediction of Flexural Strength of Concrete Produced by Using Pozzolanic Mate...



Prediction of Flexural Strength of Concrete Produced by Using Pozzolanic Mate...Journal of Soft Computing in Civil Engineering
Process Parameter Optimization for Minimizing Springback in Cold Drawing Proc...



Process Parameter Optimization for Minimizing Springback in Cold Drawing Proc...Journal of Soft Computing in Civil Engineering
COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf![COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf](https://ckxe7twkl7vq3ljkxejyz-s-a2157.bj.tsgdht.cn/ss_thumbnails/module-02notesbcg402-cgv-250506151048-aef09ce3-thumbnail.jpg?width=560&fit=bounds)
![COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf](https://ckxe7twkl7vq3ljkxejyz-s-a2157.bj.tsgdht.cn/ss_thumbnails/module-02notesbcg402-cgv-250506151048-aef09ce3-thumbnail.jpg?width=560&fit=bounds)
![COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf](https://ckxe7twkl7vq3ljkxejyz-s-a2157.bj.tsgdht.cn/ss_thumbnails/module-02notesbcg402-cgv-250506151048-aef09ce3-thumbnail.jpg?width=560&fit=bounds)
![COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdf](https://ckxe7twkl7vq3ljkxejyz-s-a2157.bj.tsgdht.cn/ss_thumbnails/module-02notesbcg402-cgv-250506151048-aef09ce3-thumbnail.jpg?width=560&fit=bounds)
COMPUTER GRAPHICS AND VISUALIZATION :MODULE-02 notes [BCG402-CG&V].pdfAlvas Institute of Engineering and technology, Moodabidri
Ad
businessstatistics-stat10022-200411201812.ppt
- 1. Basics of Statistics Definition: Science of collection, presentation, analysis, and reasonable interpretation of data. Statistics presents a rigorous scientific method for gaining insight into data. For example, suppose we measure the weight of 100 patients in a study. With so many measurements, simply looking at the data fails to provide an informative account. However statistics can give an instant overall picture of data based on graphical presentation or numerical summarization irrespective to the number of data points. Besides data summarization, another important task of statistics is to make inference and predict relations of variables. 1
- 2. Data The measurements obtained in a research study are called the data. The goal of statistics is to help researchers organize and interpret the data. 2
- 3. Descriptive statistics are methods for organizing and summarizing data. For example, tables or graphs are used to organize data, and descriptive values such as the average score are used to summarize data. A descriptive value for a population is called a parameter and a descriptive value for a sample is called a statistic. Descriptive Statistics 3
- 5. 5
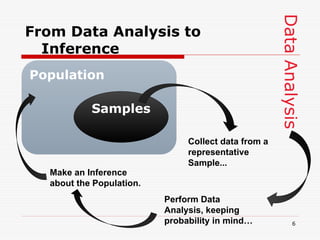
- 6. Data Analysis From Data Analysis to Inference Population Samples Collect data from a representative Sample... Perform Data Analysis, keeping probability in mind… Make an Inference about the Population. 6
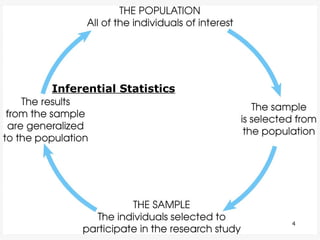
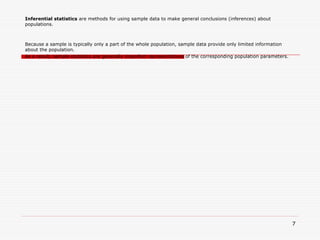
- 7. Inferential statistics are methods for using sample data to make general conclusions (inferences) about populations. Because a sample is typically only a part of the whole population, sample data provide only limited information about the population. As a result, sample statistics are generally imperfect representatives of the corresponding population parameters. 7
- 8. The discrepancy between a sample statistic and its population parameter is called sampling error. Defining and measuring sampling error is a large part of inferential statistics. Sampling Error 8
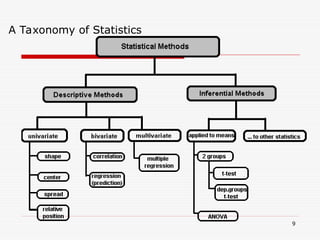
- 9. A Taxonomy of Statistics 9
- 10. Statistical Description of Data: Descriptive Statistics Statistics describes a numeric set of data by its Center Variability Shape Statistics describes a categorical set of data by Frequency, percentage or proportion of each category 10
- 11. Variable A variable is a characteristic or condition that can change or take on different values. Or any characteristic of an individual or an entity Most research begins with a general question about the relationship between two variables for a specific group of individuals. 11
- 12. Variable -. Variables can be categorical(Discrete) or quantitative(Discrete and continuous) . Categorical Variables • Nominal - Categorical variables with no inherent order or ranking sequence such as names or classes (e.g., gender, blood group). Value may be a numerical, but without numerical value (e.g., I, II, III). The only operation that can be applied to Nominal variables is enumeration (counts). • Ordinal - Variables with an inherent rank or order, e.g. mild, moderate, severe. Can be compared for equality, or greater or less, but not how much greater or less. mild, moderate or severe illness). Often ordinal variables are re- coded to be quantitative. 12
- 13. Interval - Values of the variable are ordered as in Ordinal, and additionally, differences between values are meaningful, however, the scale is not absolutely anchored. Calendar dates and temperatures on the Fahrenheit scale are examples Addition and subtraction, but not multiplication and division are meaningful operations. Ratio - Variables with all properties of Interval plus an absolute, non-arbitrary zero point, e.g. age, weight, temperature (Kelvin). Addition, subtraction, multiplication, and division are all meaningful operations. Variables (Contd) 13
- 14. Distribution Distribution - (of a variable) tells us what values the variable takes and how often it takes these values. • Unimodal - having a single peak • Bimodal - having two distinct peaks • Symmetric - left and right half are mirror images. 14
- 15. Frequency Distribution Age 1 2 3 4 5 6 Frequency 5 3 7 5 4 2 Frequency Distribution of Age Grouped Frequency Distribution of Age: Age Group 1-2 3-4 5-6 Frequency 8 12 6 Consider a data set of 26 children of ages 1-6 years. Then the frequency distribution of variable ‘age’ can be tabulated as follows: 15
- 16. Cumulative Frequency Age Group 1-2 3-4 5-6 Frequency 8 12 6 Cumulative Frequency 8 20 26 Age 1 2 3 4 5 6 Frequency 5 3 7 5 4 2 Cumulative Frequency 5 8 15 20 24 26 Cumulative frequency of data in previous slide 16
- 17. Data Presentation Two types of statistical presentation of data – Graphical Presentation and Numerical Presentation Graphical Presentation: We look for the overall pattern and for striking deviations from that pattern. Over all pattern usually described by shape, center, and spread of the data. An individual value that falls outside the overall pattern is called an Outlier. Bar diagram and Pie charts - Categorical data. Two Way Table and Conditional Distribution Histogram, Stem and Leaf Plot, Box-plot are used for numerical variable presentation. 17
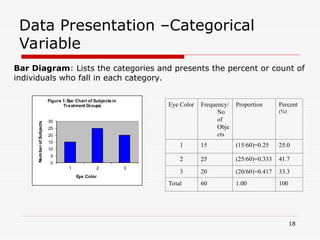
- 18. Data Presentation –Categorical Variable Bar Diagram: Lists the categories and presents the percent or count of individuals who fall in each category. Eye Color Frequency/ No of Obje cts Proportion Percent (%) 1 15 (15/60)=0.25 25.0 2 25 (25/60)=0.333 41.7 3 20 (20/60)=0.417 33.3 Total 60 1.00 100 0 5 10 15 20 25 30 1 2 3 Num ber of Subjects Eye Color Figure 1:Bar Chart of Subjects in Treatment Groups 18
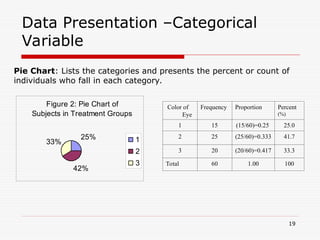
- 19. Data Presentation –Categorical Variable Pie Chart: Lists the categories and presents the percent or count of individuals who fall in each category. Figure 2: Pie Chart of Subjects in Treatment Groups 25% 42% 33% 1 2 3 Color of Eye Frequency Proportion Percent (%) 1 15 (15/60)=0.25 25.0 2 25 (25/60)=0.333 41.7 3 20 (20/60)=0.417 33.3 Total 60 1.00 100 19
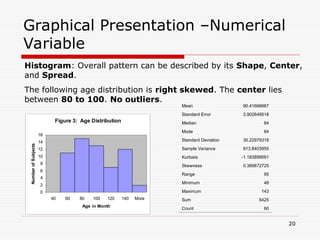
- 20. Graphical Presentation –Numerical Variable Figure 3: Age Distribution 0 2 4 6 8 10 12 14 16 40 60 80 100 120 140 More Age in Month Number of Subjects Histogram: Overall pattern can be described by its Shape, Center, and Spread. The following age distribution is right skewed. The center lies between 80 to 100. No outliers. Mean 90.41666667 Standard Error 3.902649518 Median 84 Mode 84 Standard Deviation 30.22979318 Sample Variance 913.8403955 Kurtosis -1.183899591 Skewness 0.389872725 Range 95 Minimum 48 Maximum 143 Sum 5425 Count 60 20
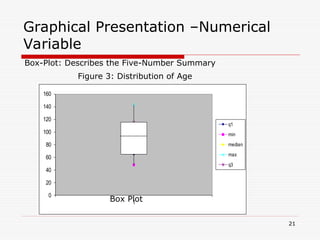
- 21. Graphical Presentation –Numerical Variable Box-Plot: Describes the Five-Number Summary 0 20 40 60 80 100 120 140 160 1 q1 min median max q3 Figure 3: Distribution of Age Box Plot 21










